题目内容
在平面直角坐标系xoy中,已知椭圆C: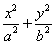 =1(a>b≥1)的离心率e=
=1(a>b≥1)的离心率e=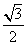 ,且椭圆C上的点到点Q (0,3)的距离最大值为4,过点M(3,0)的直线交椭圆C于点A、B.
,且椭圆C上的点到点Q (0,3)的距离最大值为4,过点M(3,0)的直线交椭圆C于点A、B.
(I)求椭圆C的方程。
(II)设P为椭圆上一点,且满足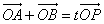 (O为坐标原点),当|AB|<
(O为坐标原点),当|AB|<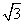 时,求实数t的取值范围.
时,求实数t的取值范围.
解:(Ⅰ)∵ ∴
∴
则椭圆方程为 即
即 设
设 则
则

 ,当
,当 时,
时,
 有最大值为
有最大值为 解得
解得 ∴
∴ ,椭圆方程是
,椭圆方程是
(Ⅱ)设
 方程为
方程为
由 整理得
整理得 .
.
由
 ,解得
,解得 .
.
 ,
,
∴ 则
则 ,
,
 , 由点P在椭圆上,代入椭圆方程得
, 由点P在椭圆上,代入椭圆方程得
 ①
①
又由 ,即
,即 ,
,
将 ,
, ,代入得
,代入得 则
则 ,
,
 , ∴
, ∴ ②
②
由①,得 ,联立②,解得
,联立②,解得
∴ 或
或

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某研究机构对高三学生的记忆力x和判断力y进行统计分析,得下表数据:
| x | 6 | 8 | 10 | 12 |
| y | 2 | 3 | 5 | 6 |
根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 中的
中的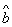 的值为
的值为 ,则记忆力为14的同学的判断力约为(附:线性回归方程
,则记忆力为14的同学的判断力约为(附:线性回归方程 中,
中, ,
,
其中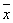 ,
, 为样本平均值)
为样本平均值)
A.7 B. C.8 D.
C.8 D.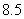
 在一个周期内的图象如图,求此函数的解析式。
在一个周期内的图象如图,求此函数的解析式。  x(x+1)(41-2x)(x≤12且x∈N*)
x(x+1)(41-2x)(x≤12且x∈N*)
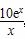 ,问:该商场销售A品牌商品,预计第几月的月利润达到最大值?月利润最大值是多少?(e6≈403)
,问:该商场销售A品牌商品,预计第几月的月利润达到最大值?月利润最大值是多少?(e6≈403)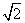 )cm2 B. 21 cm2 C.(24+4
)cm2 B. 21 cm2 C.(24+4
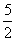 )x,若对任意的x∈[a, a+l],
)x,若对任意的x∈[a, a+l],
 c.28+
c.28+ D.26+2
D.26+2

 ,则s
,则s 的最大值为 。
的最大值为 。 ,满足条件
,满足条件 的函数是
的函数是 (B)
(B) (C)
(C) (D)
(D)