题目内容
已知圆锥的底面半径为R，高为3R，它的内接圆柱的底面半径为
，该圆柱的全面积为
- A.2πR2
- B.
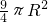
- C.
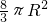
- D.
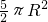
B
分析：由题意先求出内接圆柱的高，然后求该圆柱的全面积．
解答：设圆锥内接圆柱的高为h，则
，解得
，
所以圆柱的全面积为：s=2×
+
=
．
故选B．
点评：本题考查旋转体的面积，是基础题．
分析：由题意先求出内接圆柱的高，然后求该圆柱的全面积．
解答：设圆锥内接圆柱的高为h，则
，解得，所以圆柱的全面积为：s=2×
+=．故选B．
点评：本题考查旋转体的面积，是基础题．
练习册系列答案
相关题目
已知圆锥的底面半径为R，高为3R，在它的所有内接圆柱中，全面积的最大值是（ ）
| A、2πR2 | ||
B、
| ||
C、
| ||
D、
|
已知圆锥的底面半径为3，母线长为12，那么圆锥侧面展开图所成扇形的圆心角为（ ）
| A、180° | B、120° | C、90° | D、135° |