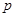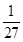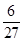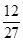Question

（本小题满分12分）

甲、乙两人各射击一次，击中目标的概率分别是和假设两人射击是否击中目标，相互

之间没有影响；每人各次射击是否击中目标，相互之间也没有影响

（1）甲射击3次，至少1次未击中目标的概率；

（2）假设某人连续2次未击中目标，则停止射击，问：乙恰好射击4次后，被中止射击的概率是多少？

⑶设甲连续射击3次，用表示甲击中目标时射击的次数，求的数学期望.（结果可以用分数表示）

 

 

 

 

Answer 1

【答案】

解：（1）记“甲连续射击3次，至少1次未击中目标”为事件A₁，由题意，射击3次，相当于3次独立重复试验，故P（A₁）=1- P（）=1-=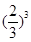

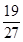
答：甲射击3次，至少1次未击中目标的概率为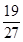；……………………4分

(2) 记“乙恰好射击4次后，被中止射击”为事件A₂，由于各事件相互独立，

故P（A₂）=×××+××× =，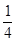

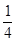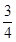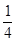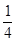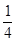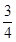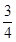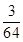答：乙恰好射击4次后，被中止射击的概率是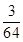……………………8分

（3）根据题意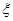服从二项分布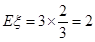，……………………12分

（3）方法二：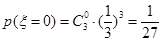   

          

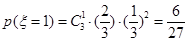
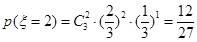
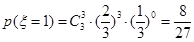
	0	1	2	3

 

 

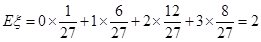……………………12分

 

【解析】略