题目内容
给出下列四个命题,其中正确命题的个数是
(1)函数f(x)=x|x|+bx+c为奇函数的充要条件是c=0;
(2)函数y=2-x的反函数是y=-log2x;
(3)若函数f(x)=lg(x2+ax-a)的值域是R,则a≤-4或a≥0;
(4)若函数y=f(x-1)是偶函数,则函数y=f(x)的图象关于直线x=1对称.
- A.1个
- B.2个
- C.3个
- D.4个
C
分析:由奇函数的定义和性质,我们可以判断(1)的真假;根据反函数的定义,易对数的运算性质,可以判断(2)的真假;根据对数函数的值域为R,则R+为x2+ax-a值域的子集,将问题转化为二次函数问题后,可判断(3)的真假;根据函数图象的平移变换法则,及偶函数的定义,可以判断(4)的真假;进而得到答案.
解答:∵y=x|x|,y=bx均为奇函数,
故函数f(x)=x|x|+bx+c为奇函数的充要条件是c=0,故(1)正确;
函数y=2-x= 的反函数是y=
的反函数是y= =y=-log2x,故(2)正确;
=y=-log2x,故(2)正确;
若函数f(x)=lg(x2+ax-a)的值域是R,则y=x2+ax-a的图象与x轴有交点,即a2+4a≥0,故a≤-4或a≥0,故(3)正确;
若函数y=f(x-1)是偶函数,则函数y=f(x)的图象关于直线x=-1对称,故(4)错误;
故选C
点评:本题考查的知识点是充要条件,反函数的定义,函数的奇偶性,函数的值域,掌握函数的三要素及三大性质是解答函数类问题的关键.
分析:由奇函数的定义和性质,我们可以判断(1)的真假;根据反函数的定义,易对数的运算性质,可以判断(2)的真假;根据对数函数的值域为R,则R+为x2+ax-a值域的子集,将问题转化为二次函数问题后,可判断(3)的真假;根据函数图象的平移变换法则,及偶函数的定义,可以判断(4)的真假;进而得到答案.
解答:∵y=x|x|,y=bx均为奇函数,
故函数f(x)=x|x|+bx+c为奇函数的充要条件是c=0,故(1)正确;
函数y=2-x=
 的反函数是y=
的反函数是y= =y=-log2x,故(2)正确;
=y=-log2x,故(2)正确;若函数f(x)=lg(x2+ax-a)的值域是R,则y=x2+ax-a的图象与x轴有交点,即a2+4a≥0,故a≤-4或a≥0,故(3)正确;
若函数y=f(x-1)是偶函数,则函数y=f(x)的图象关于直线x=-1对称,故(4)错误;
故选C
点评:本题考查的知识点是充要条件,反函数的定义,函数的奇偶性,函数的值域,掌握函数的三要素及三大性质是解答函数类问题的关键.

练习册系列答案
相关题目


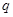 是等比数列
是等比数列 的公比,则“数列
的公比,则“数列 ”的既不充分也不必要条件;
”的既不充分也不必要条件; 上的函数
上的函数 是奇函数,则对定义域内的任意
是奇函数,则对定义域内的任意 必有
必有 ;
; 满足
满足 ,则
,则 的一个正周期为
的一个正周期为 ;
; 与
与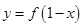 图像关于
图像关于 对称.
对称.