题目内容
己知.
(Ⅰ) 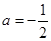 ,函数
,函数 在其定义域内是减函数,求
在其定义域内是减函数,求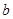 的取值范围;
的取值范围;
(Ⅱ)当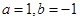 时,证明函数
时,证明函数 只有一个零点;
只有一个零点;
(Ⅲ) 若函数 的两个零点
的两个零点 ,求证:
,求证: .
.
【答案】
(Ⅰ)
(Ⅱ)证明略
(Ⅲ)证明略
【解析】(Ⅰ)依题意:
 在
在 上递减,
上递减, 对
对 恒成立[来源:学#科#网Z#X#X#K]
恒成立[来源:学#科#网Z#X#X#K]
即 对
对 恒成立,
恒成立, 只需
只需
 当且仅当
当且仅当 时取
时取

(Ⅱ)当 时,
时, ,其定义域是
,其定义域是

 时,
时, 当
当 时,
时,
 函数
函数 在区间
在区间 上单调递减,在区间
上单调递减,在区间 上单调递增
上单调递增
 当
当 时,函数
时,函数 取得最小值,即
取得最小值,即

当 时,
时,
函数 只有一个零点
只有一个零点
(Ⅲ)由已知得
 两式相减,得
两式相减,得


由


设 ,
,

 在
在 上递增,
上递增,


即

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
 ,
, (其中
(其中 ,
, ,
, )的图象与
)的图象与 轴的交点中,相邻两个交点之间的距离为
轴的交点中,相邻两个交点之间的距离为 ,且图象上一个最低点为
,且图象上一个最低点为
 的解析式。
的解析式。