Question

已知抛物线y²=4x的焦点为F，过F作斜率为

3

的直线与抛物线在x轴上方的部分交于M点，过M作y轴的垂线，垂足为N，则线段NF的长度为（　　）

• A．2

  3

• B．4
• C．4

  3

• D．

  13

Answer 1

分析：先判断△MKF为等边三角形，求出M的坐标，可求出等边△MKF的边长AK=m+1的值，从而求出点M的坐标及点N的坐标，
由两点间的距离公式求出NF的长度．

解答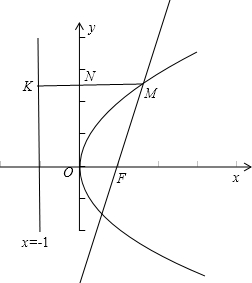：解：抛物线y²=4x的焦点为F（1，0），准线方程为x=-1，延长MN交准线l于K．
由抛物线的定义可得MF=MK，∵MF的斜率等于

3

，∴MF的倾斜角等于60°，∵MK⊥l，
∴∠FMK=60°，故△MKF为等边三角形，MF的方程为 y-0=

3

（x-1），
设M（m，

3

m-

3

），m＞1，由|MF|=|MK|得 

(m-1)2+( 3 m- 3 )2

=m+1，
∴m=3，故等边三角形△MKF的边长|MK|=m+1=4，M（3，2

3

）、N（0，2

3

）．
故|NF|=

(1-0)2+(0-2 3 )2

=

13

．
故选D．

点评：本题考查抛物线的定义、标准方程，以及简单性质的应用，判断△MKF为等边三角形是解题的关键．