题目内容
已知数列 满足
满足 ,
, ,数列
,数列 满足
满足 。
。
(1)求数列 的通项公式;
的通项公式;
(2)设数列 的前n项和为
的前n项和为 ,求证:当
,求证:当 时,
时, ;
;
(3)求证:当 时,
时, 。
。
 满足
满足 ,
, ,数列
,数列 满足
满足 。
。(1)求数列
 的通项公式;
的通项公式;(2)设数列
 的前n项和为
的前n项和为 ,求证:当
,求证:当 时,
时, ;
;(3)求证:当
 时,
时, 。
。 (1)解:由题意,得 ,
,
即 ,
,
∴ 。
。
(2)解:由(1)知, ,
,
当 时,
时, ,即
,即 ,
,
平方,得 ,
,
∴ ,
,
叠加,得 ,
,
∴ ,
,
∴ 。
。
(3)证明:当n=2时, ,即n=2时,命题成立;
,即n=2时,命题成立;
假设 命题成立,即
命题成立,即
 ,
,
当 时,
时,

 ,
,
即 时,命题成立;
时,命题成立;
综上,对于任意 ,
, 。
。
 ,
,即
 ,
,∴
 。
。(2)解:由(1)知,
 ,
,当
 时,
时, ,即
,即 ,
,平方,得
 ,
,∴
 ,
,叠加,得
 ,
,∴
 ,
,∴
 。
。(3)证明:当n=2时,
 ,即n=2时,命题成立;
,即n=2时,命题成立;假设
 命题成立,即
命题成立,即 ,
,当
 时,
时,
 ,
,即
 时,命题成立;
时,命题成立;综上,对于任意
 ,
, 。
。
练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 满足
满足 ,
, ;数列
;数列 满足
满足 ,
,  .
. 和
和 的通项公式;
的通项公式; 、
、 的前
的前 项和
项和 ,
, .
. 满足
满足 ,则数列
,则数列 _______________.
_______________.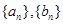 满足:
满足: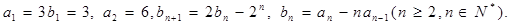
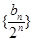 是等差数列还是等比数列,并由此求数列
是等差数列还是等比数列,并由此求数列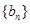 的通项公式;
的通项公式;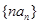 的前n项和
的前n项和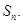
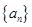 为等比数列,且其满足:
为等比数列,且其满足: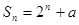 .
.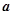 的值及数列
的值及数列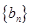 满足
满足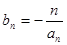 ,求数列
,求数列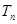 .
.