题目内容
(本小题满分10分)等差数列 中,
中, ,公差
,公差 且
且 成等比数列,前
成等比数列,前 项的和为
项的和为 .
.
(1)求 及
及 ;
;
(2)设 ,
, ,求
,求 .
.
(1) ,
, ;(2)
;(2) .
.
解析试题分析:(1)首先根据a1=-1和d,求出 ,再根据
,再根据 是等比数列,求出数列{an}的通项公式,再由等比数列的前n项和公式即可求得
是等比数列,求出数列{an}的通项公式,再由等比数列的前n项和公式即可求得 ;
;
(2)根据(1)求出数列{bn}的通项公式,然后根据数列通项公式的特点选用裂项求和法进行求和即可.
试题解析:(1)有题意可得 又因为
又因为
 2分
2分
 4分
4分
(2) 6分
6分
 10分
10分
考点:1.等比数列;2.数列求和.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
一算法的程序框图如图所示,若输出的 ,则输入的
,则输入的 可能为
可能为
A. | B. | C. | D. |
已知直线
 平行,则它们之间的距离是( )
平行,则它们之间的距离是( )
| A.1 | B.2 | C. | D.4 |
下面一段程序执行后输出结果是( )
A=2
A=A*2
A=A+6
PRINT A
| A.2 | B.8 | C.10 | D.18 |
 ,其中
,其中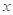 是仪器的月产量,
是仪器的月产量,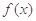 表示为月产量
表示为月产量 与
与 的夹角为
的夹角为 ,
, ,
, ,则
,则 = .
= . ,
, ,若
,若 ,则
,则 .
. 的前n项和
的前n项和 ,则
,则 = .
= . 的公差不为0,其前
的公差不为0,其前 的前
的前 ,公比为
,公比为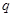 ,且
,且 ,求
,求 的值
的值