题目内容
已知函数 定义域为D,且方程f(x)=x在D上有两个不等实根,则k的取值范围是( )
定义域为D,且方程f(x)=x在D上有两个不等实根,则k的取值范围是( )A.-1<k≤

B.
 ≤k<1
≤k<1C.k>-1
D.k<1
【答案】分析:根据函数 ,我们可得方程f(x)=x的表达式,
,我们可得方程f(x)=x的表达式,
(法一)我们可以根据方程的根与函数零点的对应关系,将问题转化为两个函数图象有两个交点的问题,然后分析临界直线性质,构造关于k的不等式,解不等式即可得到答案.
(法二)利用平方法去掉绝对值符号后,将问题转化为一个二次方程在定区间有两相异实根问题,构造函数,利用二次函数的性质,构造关于k的不等式,解不等式即可得到答案.
解答: 解:依题意
解:依题意 在
在 上有两个不等实根.
上有两个不等实根.
(方法一)问题可化为 和y=x-k在
和y=x-k在 上有两个不同交点、
上有两个不同交点、
对于临界直线m,应有-k≥ ,即k≤
,即k≤ .
.
对于临界直线n,化简方程 ,
,
得x2-(2k+2)x+k2-1=0,
令△=0,解得k=-1,
∴n:y=x+1,令x=0,得y=1,
∴-k<1,即k>-1.
综上,-1<k≤ .
.
(方法二)化简方程 ,
,
得x2-(2k+2)x+k2-1=0.
令g(x)=x2-(2k+2)x+k2-1,
则由根的分布可得 ,即
,即 ,
,
解得k>-1.又 ,
,
∴x≥k,∴k≤ .
.
综上,-1<k≤ .
.
点评:本题考查的知识点是根的存在性及根的个数判断,其中根据已知条件,构造关于k的不等式,是解答本题的关键.
 ,我们可得方程f(x)=x的表达式,
,我们可得方程f(x)=x的表达式,(法一)我们可以根据方程的根与函数零点的对应关系,将问题转化为两个函数图象有两个交点的问题,然后分析临界直线性质,构造关于k的不等式,解不等式即可得到答案.
(法二)利用平方法去掉绝对值符号后,将问题转化为一个二次方程在定区间有两相异实根问题,构造函数,利用二次函数的性质,构造关于k的不等式,解不等式即可得到答案.
解答:
 解:依题意
解:依题意 在
在 上有两个不等实根.
上有两个不等实根.(方法一)问题可化为
 和y=x-k在
和y=x-k在 上有两个不同交点、
上有两个不同交点、对于临界直线m,应有-k≥
 ,即k≤
,即k≤ .
.对于临界直线n,化简方程
 ,
,得x2-(2k+2)x+k2-1=0,
令△=0,解得k=-1,
∴n:y=x+1,令x=0,得y=1,
∴-k<1,即k>-1.
综上,-1<k≤
 .
.(方法二)化简方程
 ,
,得x2-(2k+2)x+k2-1=0.
令g(x)=x2-(2k+2)x+k2-1,
则由根的分布可得
 ,即
,即 ,
,解得k>-1.又
 ,
,∴x≥k,∴k≤
 .
.综上,-1<k≤
 .
.点评:本题考查的知识点是根的存在性及根的个数判断,其中根据已知条件,构造关于k的不等式,是解答本题的关键.

练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
 定义域为D,且方程
定义域为D,且方程 在D上有两个不等实根,则k的取值范围是
在D上有两个不等实根,则k的取值范围是 B.
B. C.
C.  D.
D. [来源:Z
[来源:Z D,存在正数k,有|f(x)|≤k|x|成立,则称函数f(x)是D上的“倍约束函数”,已知下列函数:(1)f(x)=2x; (2)f(x)=Sin(x+
D,存在正数k,有|f(x)|≤k|x|成立,则称函数f(x)是D上的“倍约束函数”,已知下列函数:(1)f(x)=2x; (2)f(x)=Sin(x+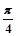 );(3)f(x)=
);(3)f(x)=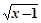 ;(4)f(x)=
;(4)f(x)= ;其中是“倍约束函数”的是( )
;其中是“倍约束函数”的是( ) D,存在正数k,有|f(x)|≤k|x|成立,则称函数f(x)是D上的“倍约束函数”,已知下列函数:(1)f(x)=2x; (2)f(x)=Sin(x+
D,存在正数k,有|f(x)|≤k|x|成立,则称函数f(x)是D上的“倍约束函数”,已知下列函数:(1)f(x)=2x; (2)f(x)=Sin(x+ );(3)f(x)=
);(3)f(x)= ;(4)f(x)=
;(4)f(x)=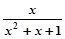 ;其中是“倍约束函数”的是(
)
;其中是“倍约束函数”的是(
) 定义域为D,且方程f(x)=x在D上有两个不等实根,则k的取值范围是( )
定义域为D,且方程f(x)=x在D上有两个不等实根,则k的取值范围是( )
 ≤k<1
≤k<1