题目内容
已知数列{an}满足a1=2,且an= .
.
(1)求数列{an}的通项公式;
(2)对一切正整数n,令Sn=a1a2+a2a3+…+anan+1,求Sn.
解:(1)由an=
可得
即
∴数列{ }是以
}是以 为首项,以1为公差的等差数列
为首项,以1为公差的等差数列
∴
∴
(2)∵anan+1= =2(
=2(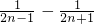 )
)
∴
=2(1- )=
)=
分析:(1)由an= 可构造等差数列,可求
可构造等差数列,可求 ,进而可求an
,进而可求an
(2)结合数列的特点,考虑利用裂项求和方法即可求解
点评:本题主要考查了利用数列的递推公式构造等差数列,数列的裂项求和方法的应用是求和的关键

可得

即

∴数列{
 }是以
}是以 为首项,以1为公差的等差数列
为首项,以1为公差的等差数列∴

∴

(2)∵anan+1=
 =2(
=2(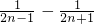 )
)∴

=2(1-
 )=
)=
分析:(1)由an=
 可构造等差数列,可求
可构造等差数列,可求 ,进而可求an
,进而可求an(2)结合数列的特点,考虑利用裂项求和方法即可求解
点评:本题主要考查了利用数列的递推公式构造等差数列,数列的裂项求和方法的应用是求和的关键

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目