题目内容
奇函数f(x)在(-1,1)上是单调递减的,若f(1-m)+f(1-m2)<0,则实数m的取值范围是
- A.(0,1)
- B.(-2,1)
- C.
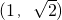
- D.(-1,1)
A
分析:先将不等式移项变形,再利用函数的单调性,得到不等关系,注意到函数的定义域.
解答:奇函数f(x)在(-1,1)上是单调递减的,由f(1-m)+f(1-m2)<0,得
f(1-m)<-f(1-m2)=f(m2-1),又f(x)在(-1,1)单调递减
∴1-m>m2-1 ①
又-1<1-m<1 ②
-1<1-m2<1 ③
综合①②③,解得
0<m<1
故选:A.
点评:本题是对函数单调性和奇偶性的综合考查,属于历年来常见的考题,只要利用相应性质适当变形即可.解题时,学生往往容易忽视函数的定义域而使解答有误.
分析:先将不等式移项变形,再利用函数的单调性,得到不等关系,注意到函数的定义域.
解答:奇函数f(x)在(-1,1)上是单调递减的,由f(1-m)+f(1-m2)<0,得
f(1-m)<-f(1-m2)=f(m2-1),又f(x)在(-1,1)单调递减
∴1-m>m2-1 ①
又-1<1-m<1 ②
-1<1-m2<1 ③
综合①②③,解得
0<m<1
故选:A.
点评:本题是对函数单调性和奇偶性的综合考查,属于历年来常见的考题,只要利用相应性质适当变形即可.解题时,学生往往容易忽视函数的定义域而使解答有误.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目