题目内容
(已知抛物线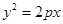 (
(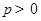 )的准线与
)的准线与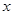 轴交于点
轴交于点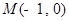 .
.
(1)求抛物线的方程,并写出焦点坐标;
(2)是否存在过焦点的直线 (直线与抛物线交于点
(直线与抛物线交于点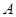 ,
, ),使得三角形
),使得三角形 的面积
的面积 ?若存在,请求出直线
?若存在,请求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(1)参考解析;(2)存在, 或
或
解析试题分析:(1)由抛物线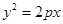 (
(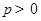 )的准线与
)的准线与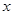 轴交于点
轴交于点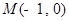 ,可求得
,可求得 的值,即可得到抛物线方程与焦点坐标
的值,即可得到抛物线方程与焦点坐标
(2)由于过焦点的直线 可能垂直于x轴,依题意不可能垂直于y轴,所以假设直线
可能垂直于x轴,依题意不可能垂直于y轴,所以假设直线
 .再联立抛物线方程,由韦达定理以及弦长公式即可得到AB的弦长.由点到直线的距离公式即可得到点M到直线AB的距离.再由
.再联立抛物线方程,由韦达定理以及弦长公式即可得到AB的弦长.由点到直线的距离公式即可得到点M到直线AB的距离.再由 即可求出结论.
即可求出结论.
解法一:(1)由已知得: ,从而抛物线方程为
,从而抛物线方程为 ,
,
焦点坐标为 . 4分
. 4分
(2)由题意,设
 ,并与
,并与 联立,
联立,
得到方程: , 6分
, 6分
设 ,
, ,则
,则 ,
, . 7分
. 7分
∵ ,∴
,∴

 , 9分
, 9分
又 ,∴
,∴ 10分
10分
解得 , 11分
, 11分
故直线 的方程为:
的方程为: .即
.即 或
或 . 12分
. 12分
解法二:(1)(同解法一)
(2)当 轴时,
轴时, ,
, ,
,
不符合题意. 5分
故设
 (
( ),并与
),并与 联立,
联立,
得到方程: , 6分
, 6分
设 ,
, ,则
,则 ,
, . 7分
. 7分
 ,
,
点 到直线
到直线 的距离为
的距离为 , 9分
, 9分
∴

 , 10分
, 10分
解得 , &n
, &n

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
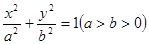 的离心率为
的离心率为 ,点
,点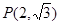 在椭圆上.
在椭圆上.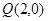 的动直线与椭圆交于M,N两点,连接AN、BM相交于G点,试求点G的横坐标的值.
的动直线与椭圆交于M,N两点,连接AN、BM相交于G点,试求点G的横坐标的值.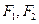 分别是椭圆
分别是椭圆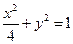 的 左,右焦点。
的 左,右焦点。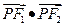 的 最大值和最小值。
的 最大值和最小值。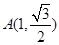 ,两焦点为
,两焦点为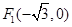 、
、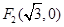 ,
,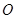 是坐标原点,不经过原点的直线
是坐标原点,不经过原点的直线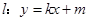 与该椭圆交于两个不同点
与该椭圆交于两个不同点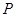 、
、 ,且直线
,且直线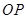 、
、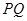 、
、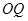 的斜率依次成等比数列.
的斜率依次成等比数列.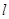 的斜率
的斜率 ;
;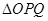 面积的范围.
面积的范围.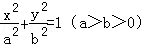 的离心率
的离心率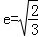 ,且椭圆C上的点到点Q(0,2)的距离的最大值为3.
,且椭圆C上的点到点Q(0,2)的距离的最大值为3.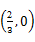 ,求曲线上距点A最近的点P的坐标及相应的距离|PA|.
,求曲线上距点A最近的点P的坐标及相应的距离|PA|. 的左焦点为F1(-1,0),且点P(0,1)在C1上。
的左焦点为F1(-1,0),且点P(0,1)在C1上。 相切,求直线l的方程.
相切,求直线l的方程. 的离心率为
的离心率为 ,
, 轴被曲线
轴被曲线 截得的线段长等于
截得的线段长等于 的长半轴长。
的长半轴长。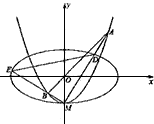
 的方程;
的方程; 轴的交点为M,过坐标原点O的直线
轴的交点为M,过坐标原点O的直线 与
与 ;
; .问:是否存在直线
.问:是否存在直线 =
= ?请说明理由。
?请说明理由。 的离心率为
的离心率为 ,以原点为圆心、椭圆的短半轴长为半径的圆与直线
,以原点为圆心、椭圆的短半轴长为半径的圆与直线 相切.
相切. 的方程;
的方程; ,过点
,过点 作直线
作直线 (不与
(不与 轴重合)交椭圆于
轴重合)交椭圆于 、
、 两点,连结
两点,连结 、
、 分别交直线
分别交直线 于
于 、
、 两点,试探究直线
两点,试探究直线 、
、 的斜率之积是否为定值,若为定值,请求出;若不为定值,请说明理由.
的斜率之积是否为定值,若为定值,请求出;若不为定值,请说明理由.