题目内容
(2013•蓟县二模)已知数列{an}的首项a1=1,a2=3,前n项和为Sn,且
=
,(n∈N*,n≥2),数列{bn}满足b1=1,bn+1=log2(an+1)+bn.
(Ⅰ)判断数列{an+1}是否为等比数列,并证明你的结论;
(Ⅱ)设cn=-an(bn-
-1),求c1+c2+c3+…+cn;
(Ⅲ)对于(Ⅰ)中数列{an},若数列{ln}满足ln=log2(an+1)(n∈N*),在每两个lk与lk+1之间都插入2k-1(k=1,2,3,…k∈N*)个2,使得数列{ln}变成了一个新的数列{tp},(p∈N*)试问:是否存在正整数m,使得数列{tp}的前m项的和Tm=2011?如果存在,求出m的值;如果不存在,说明理由.
| Sn+1-Sn |
| Sn-Sn-1 |
| 2an+1 |
| an |
(Ⅰ)判断数列{an+1}是否为等比数列,并证明你的结论;
(Ⅱ)设cn=-an(bn-
| n2 |
| 2 |
(Ⅲ)对于(Ⅰ)中数列{an},若数列{ln}满足ln=log2(an+1)(n∈N*),在每两个lk与lk+1之间都插入2k-1(k=1,2,3,…k∈N*)个2,使得数列{ln}变成了一个新的数列{tp},(p∈N*)试问:是否存在正整数m,使得数列{tp}的前m项的和Tm=2011?如果存在,求出m的值;如果不存在,说明理由.
分析:(I)根据已知等式,将an=Sn-Sn-1和an+1=Sn+1-Sn代入,化简整理得an+1=2an+1,由此即可证出数列{an+1}是公比为2的等比数列;
(II)根据(I)的结论算出an=2n-1,利用对数的运算法则算出bn+1-bn=n,采用累加的方法算出bn=1+
.从而化简出c n=n•2n-1-
,利用错位相减法并结合等差数列的求和公式,即可算出c1+c2+c3+…+cn的值;
(II)首先根据an通项公式算出ln=n(n∈N*),结合题意利用等差、等比数列的求和公式算出得到数列{tn}中,lk(含其本身)前的所有项之和等于
+2k-2.再验证当k=10时,和为1077<2011;
当k=11时,和为2112>2011.从而得到2011项在k=10与k=11之间,而2011-1077=467×2恰好为2的整数倍,由此加以计算即可得到存在m=998,使得Tm=2011.
(II)根据(I)的结论算出an=2n-1,利用对数的运算法则算出bn+1-bn=n,采用累加的方法算出bn=1+
| n(n-1) |
| 2 |
| n |
| 2 |
(II)首先根据an通项公式算出ln=n(n∈N*),结合题意利用等差、等比数列的求和公式算出得到数列{tn}中,lk(含其本身)前的所有项之和等于
| k(k+1) |
| 2 |
当k=11时,和为2112>2011.从而得到2011项在k=10与k=11之间,而2011-1077=467×2恰好为2的整数倍,由此加以计算即可得到存在m=998,使得Tm=2011.
解答:解:(I)∵
=
∴
=
,化简得an+1=2an+1
由此可得an+1+1=2an+2=2(an+1)
∴数列{an+1}是公比为2的等比数列;
(II)由(I),得an+1=(a1+1)•2n-1
∵a1+1=2,∴an+1=2•2n-1=2n,因此an=2n-1,
得bn+1=log2(an+1)+bn,即bn+1=log22n+bn,bn+1=n+bn,
∴bn+1-bn=n,分别取n=1、2、3、…、n-1
得bn=b1+(b2-b1)+(b3-b2)+(b4-b3)+…+(bn-bn-1)
=1+[1+2+3+…+(n-1)]=1+
∴cn=-an(bn-
-1)=(2n-1)•
=n•2n-1-
令An=1•20+2•21+3•22+…+n•2n-1①
可得2An=1•21+2•22+3•23+…+n•2n②…(6分)
①-②得-An=1+21+22+23+…+2n-1-n•2n…(7分)
∴-An=
-n•2n=2n-1-n•2n,整理得An=(n-1)2n+1
令Bn=
(1+2+3+…+n)=
∴c1+c2+…+cn=An-Bn=(n-1)2n+1-
…(10分)
(I)∵ln=log2(an+1)=log22n=n(n∈N*)
数列{tn}中,lk(含其本身)前的所有项之和为:
(1+2+3+…+k)+2(20+21+22+…+2k-2)=
+2k-2
当k=10时,其和为55+210-2=1077<2011;
当k=11时,其和为66+211-2=2112>2011
又∵2011-1077=467×2,恰好为2的整数倍
∴当m=10+(1+2+22+…+28)+467=988时,Tm=2011
综上所述,得存在m=998,使得Tm=2011.
| Sn+1-Sn |
| Sn-Sn-1 |
| 2an+1 |
| an |
∴
| an+1 |
| an |
| 2an+1 |
| an |
由此可得an+1+1=2an+2=2(an+1)
∴数列{an+1}是公比为2的等比数列;
(II)由(I),得an+1=(a1+1)•2n-1
∵a1+1=2,∴an+1=2•2n-1=2n,因此an=2n-1,
得bn+1=log2(an+1)+bn,即bn+1=log22n+bn,bn+1=n+bn,
∴bn+1-bn=n,分别取n=1、2、3、…、n-1
得bn=b1+(b2-b1)+(b3-b2)+(b4-b3)+…+(bn-bn-1)
=1+[1+2+3+…+(n-1)]=1+
| n(n-1) |
| 2 |
∴cn=-an(bn-
| n2 |
| 2 |
| n |
| 2 |
| n |
| 2 |
令An=1•20+2•21+3•22+…+n•2n-1①
可得2An=1•21+2•22+3•23+…+n•2n②…(6分)
①-②得-An=1+21+22+23+…+2n-1-n•2n…(7分)
∴-An=
| 1-2n |
| 1-2 |
令Bn=
| 1 |
| 2 |
| n(n+1) |
| 4 |
∴c1+c2+…+cn=An-Bn=(n-1)2n+1-
| n(n+1) |
| 4 |
(I)∵ln=log2(an+1)=log22n=n(n∈N*)
数列{tn}中,lk(含其本身)前的所有项之和为:
(1+2+3+…+k)+2(20+21+22+…+2k-2)=
| k(k+1) |
| 2 |
当k=10时,其和为55+210-2=1077<2011;
当k=11时,其和为66+211-2=2112>2011
又∵2011-1077=467×2,恰好为2的整数倍
∴当m=10+(1+2+22+…+28)+467=988时,Tm=2011
综上所述,得存在m=998,使得Tm=2011.
点评:本题着重考查了等差、等比数列的通项公式与求和公式、数列的通项与求和和对数的运算法则等知识,考查了转化、化归与函数方程数学思想的应用,属于中档题.

练习册系列答案
相关题目
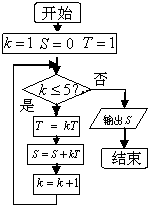 (2013•蓟县二模)如果执行如面的程序框图,那么输出的S=( )
(2013•蓟县二模)如果执行如面的程序框图,那么输出的S=( )