题目内容
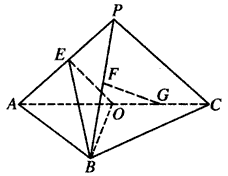
如图,平面PAC⊥平面ABC,点E,F,D分别为线段PA,PB,AC的中点,点G是线段CO的中点,AB=BC=AC=4,PA=PC=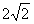 ,
,
求证:(Ⅰ)PA⊥平面EBO;
(Ⅱ)FG∥平面EBO。
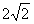 ,
,求证:(Ⅰ)PA⊥平面EBO;
(Ⅱ)FG∥平面EBO。
| 证明:由题意可知,△PAC为等腰直角三角形, △ABC为等边三角形, (Ⅰ)因为O为边AC的中点,所以BO⊥AC, 因为平面PAC⊥平面ABC,平面PAC∩平面ABC=AC, BO  平面ABC, 平面ABC,所以BO⊥面PAC, 因为PA  平面PAC,所以BO⊥PA, 平面PAC,所以BO⊥PA,在等腰三角形PAC内,O,E为所在边的中点, 所以OE⊥PA, 又BO∩OE=O, 所以PA⊥平面EBO; |
|
| (Ⅱ)连接AF交BE于Q,连接QO, 因为E,F,O分别为边PA,PB,AC的中点, 所以  ,且Q是△PAB的重心, ,且Q是△PAB的重心,于是  , ,所以FG∥QO, 因为FG  平面EBO,QO 平面EBO,QO 平面EBO, 平面EBO,所以FG∥平面EBO。 |
 |

练习册系列答案
相关题目
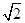 倍,
倍,
 倍,
倍, P为侧棱SD上的点。(Ⅰ)求证:AC⊥SD;
P为侧棱SD上的点。(Ⅰ)求证:AC⊥SD;