题目内容
设数列{an}的前n项和为Sn,已知a1=1,Sn+1=4an+2(1)设bn=an+1-2an,证明数列{bn}是等比数列
(2)求数列{nbn}的前n项和Tn.
【答案】分析:(1)先根据Sn+1=4an+2,得到Sn=4an-1+3,两式相减得到an+1=4an-4an-1 ,再变形得an+1-2an=2(an-2an-1),令n=1求出a2的值,由等比数列的定义得{an-2an-1}是以3为首项,2为公比的等比数列,即数列{bn}是等比数列;
(2)先由(1)和等比数列的通项公式,求出数列{nbn}的通项公式,再利用错位相减法求数列{nbn}的前n项和Tn.
解答:解:(1)由题意知,Sn+1=4an+2 ①
∴Sn=4an-1+2 (n≥2)②
①-②:an+1=4an-4an-1
∴an+1-2an=2(an-2an-1)
令n=1得,s2=4a1+2=a1+a2,解得a2=5,
数列{an-2an-1}是以3为首项,2为公比的等比数列,
∵bn=an+1-2an,
∴数列{bn}是等比数列,
(2)由(1)得,bn=an+1-2an=3•2n-1,
∴nbn=3n•2n-1
∴Tn=3[1×2+2×21+3×22+…+n•2n-1]③
∴2Tn=3[1×21+2×22+…+(n-1)•2n-1+n•2n]④
③-④:-Tn=3[1+21+22+23+…+2n-1-n•2n]
=3×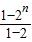 -3n•2n=(3-3n)•2n-3,
-3n•2n=(3-3n)•2n-3,
∴Tn=(3n-3)•2n+3.
点评:本题主要考查数列通项公式与前n项和之间的关系,等比数列的通项公式和前n项和公式,以及错位相减法求和,考查了计算能力.
(2)先由(1)和等比数列的通项公式,求出数列{nbn}的通项公式,再利用错位相减法求数列{nbn}的前n项和Tn.
解答:解:(1)由题意知,Sn+1=4an+2 ①
∴Sn=4an-1+2 (n≥2)②
①-②:an+1=4an-4an-1
∴an+1-2an=2(an-2an-1)
令n=1得,s2=4a1+2=a1+a2,解得a2=5,
数列{an-2an-1}是以3为首项,2为公比的等比数列,
∵bn=an+1-2an,
∴数列{bn}是等比数列,
(2)由(1)得,bn=an+1-2an=3•2n-1,
∴nbn=3n•2n-1
∴Tn=3[1×2+2×21+3×22+…+n•2n-1]③
∴2Tn=3[1×21+2×22+…+(n-1)•2n-1+n•2n]④
③-④:-Tn=3[1+21+22+23+…+2n-1-n•2n]
=3×
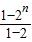 -3n•2n=(3-3n)•2n-3,
-3n•2n=(3-3n)•2n-3,∴Tn=(3n-3)•2n+3.
点评:本题主要考查数列通项公式与前n项和之间的关系,等比数列的通项公式和前n项和公式,以及错位相减法求和,考查了计算能力.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目