题目内容
 三棱锥V-ABC中,VA=VB=AC=BC=2,AB=2
三棱锥V-ABC中,VA=VB=AC=BC=2,AB=2| 3 |
分析:根据题意,证出∠CDV就是二面角V-AB-C的平面角,且△VCD是正三角形,得A项不错;根据线面垂直的判定定理证出AB⊥平面VCD,从而得到直线AB、VC所成的角为90°,故B项不错;利用中位线,结合异面直线所成角的定义证出AC、VB所成的角的余弦值等于
,说明直线AC、VB所成的角不是60°,故C项错误;根据锥体体积公式结合题中数据算出三棱锥V-ABC的体积为
,故D项也不错.由此得到本题答案.
| 5 |
| 8 |
| 1 |
| 2 |
解答:解:∵等腰△VAB与等腰△ABC有公共的底边AB,D为AB中点,
∴VD⊥AB且CD⊥AB,可得∠CDV就是二面角V-AB-C的平面角
∵VC=CD=VD=1,
∴△VCD是正三角形,得∠CDV=60°.故A不错;
∵VD⊥AB,CD⊥AB,VD、CD是平面VCD内的相交直线
∴AB⊥平面VCD,结合VC?平面VCD得AB⊥VC
即直线AB、VC所成的角为90°,故B不错;
取VC、BC的中点E、F,连结DE、DF、EF
可得∠DFE或其补角就是直线AC、VB所成的角
∵△DFE中,DE=EF=1,DE=
∴cos∠DFE=
=
,可得∠DFE≠60°,故C项错误;
对于D,由前面的分析可得三棱锥V-ABC的体积为
V=
×S△VCD×AB=
×
×2
=
,故D项不错
故选:C

∴VD⊥AB且CD⊥AB,可得∠CDV就是二面角V-AB-C的平面角
∵VC=CD=VD=1,
∴△VCD是正三角形,得∠CDV=60°.故A不错;
∵VD⊥AB,CD⊥AB,VD、CD是平面VCD内的相交直线
∴AB⊥平面VCD,结合VC?平面VCD得AB⊥VC
即直线AB、VC所成的角为90°,故B不错;
取VC、BC的中点E、F,连结DE、DF、EF
可得∠DFE或其补角就是直线AC、VB所成的角
∵△DFE中,DE=EF=1,DE=
| ||
| 2 |
∴cos∠DFE=
1+1-
| ||
| 2×1×1 |
| 5 |
| 8 |
对于D,由前面的分析可得三棱锥V-ABC的体积为
V=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 4 |
| 3 |
| 1 |
| 2 |
故选:C
点评:本题给出特殊三棱锥,求线面角、线线角、面面角并求锥体的体积.着重考查了二面角的定义与求法、异面直线所成角的定义和锥体体积公式等知识,属于中档题.

练习册系列答案
相关题目
 15、如图,三棱锥V-ABC中,VA⊥底面ABC,∠ABC=90°.
15、如图,三棱锥V-ABC中,VA⊥底面ABC,∠ABC=90°.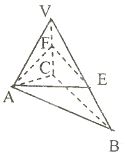 如图所示,侧棱长为
如图所示,侧棱长为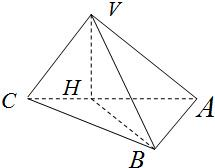 在三棱锥V-ABC中,底面△ABC是以∠ABC为直角的等腰三角形.又V在底面ABC上的射影H在线段AC上且靠近点C,AC=4,
在三棱锥V-ABC中,底面△ABC是以∠ABC为直角的等腰三角形.又V在底面ABC上的射影H在线段AC上且靠近点C,AC=4,