题目内容
若函数f（x）=
的定义域为R，则a的取值范围为________．
[-1，0]
分析：由函数f（x）=的定义域为R，知x2-2ax-a≥0的解集为R，由此能求出a的取值范围．
解答：∵函数f（x）=的定义域为R，
∴x2-2ax-a≥0的解集为R，
∴△=4a2+4a≤0，
解得-1≤a≤0．
故答案为：[-1，0]．
点评：本题考查函数的定义域的求法，是基础题．解题时要认真审题，仔细解答，注意一元二次不等式的应用．
分析：由函数f（x）=
的定义域为R，知x2-2ax-a≥0的解集为R，由此能求出a的取值范围．解答：∵函数f（x）=
的定义域为R，∴x2-2ax-a≥0的解集为R，
∴△=4a2+4a≤0，
解得-1≤a≤0．
故答案为：[-1，0]．
点评：本题考查函数的定义域的求法，是基础题．解题时要认真审题，仔细解答，注意一元二次不等式的应用．
练习册系列答案
相关题目
．
．
与
的大小，并说明你的理由．
．
．
与
的大小，并说明你的理由．
．
．
与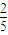
的大小，并说明你的理由．