题目内容
(14分)已知a,b是实数,函数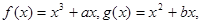
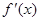 和
和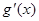 是
是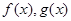 的导函数,若
的导函数,若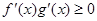 在区间
在区间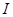 上恒成立,则称
上恒成立,则称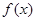 和
和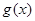 在区间
在区间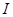 上单调性一致
上单调性一致
(1)设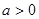 ,若
,若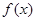 和
和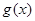 在区间
在区间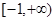 上单调性一致,求b的取值范围;
上单调性一致,求b的取值范围;
(2)设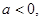 且
且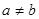 ,若
,若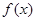 和
和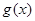 在以a,b为端点的开区间上单调性一致,求|a―b|的最大值
在以a,b为端点的开区间上单调性一致,求|a―b|的最大值
【答案】

(1)由题意知 上恒成立,因为a>0,故
上恒成立,因为a>0,故
进而 上恒成立,所以
上恒成立,所以
因此 的取值范围是
的取值范围是 [
[
(2)令
若 又因为
又因为 ,
,
所以函数 在
在 上不是单调性一致的,因此
上不是单调性一致的,因此
现设 ;
;
当 时,
时,
因此,当 时,
时,
故由题设得
从而
因此 时等号成立,
时等号成立,
又当 ,从而当
,从而当
故当函数 上单调性一致,因此
上单调性一致,因此 的最大值为
的最大值为

(1)由题意知 上恒成立,因为a>0,故
上恒成立,因为a>0,故
进而 上恒成立,所以
上恒成立,所以
因此 的取值范围是
的取值范围是 [
[
(2)令
若 又因为
又因为 ,
,
所以函数 在
在 上不是单调性一致的,因此
上不是单调性一致的,因此
现设 ;
;
当 时,
时,
因此,当 时,
时,
故由题设得
从而
因此 时等号成立,
时等号成立,
又当 ,从而当
,从而当
故当函数 上单调性一致,因此
上单调性一致,因此 的最大值为
的最大值为
【解析】略

练习册系列答案
相关题目
 =(x,1),
=(x,1), =(-1,b-x),函数f(x)=a-
=(-1,b-x),函数f(x)=a-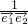 是偶函数.
是偶函数. =(x,1),
=(x,1), =(-1,b-x),函数f(x)=a-
=(-1,b-x),函数f(x)=a- 是偶函数.
是偶函数.