题目内容
观察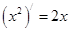 ,
,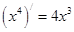 ,
,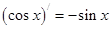 ,由归纳推理可得:若定义在
,由归纳推理可得:若定义在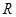 上的函数
上的函数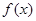 满足
满足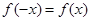 ,记
,记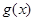 为
为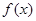 的导函数,则
的导函数,则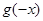 =( )
=( )
A.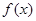 | B.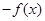 | C.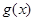 | D.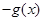 |
D
解析试题分析:由给出的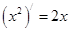 ,
,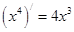 ,
,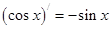 三个例子,可分别记为
三个例子,可分别记为 ,
, ,
, ,它们的定义域都为
,它们的定义域都为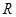 ,且满足
,且满足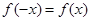 ;则三个函数的导函数分别记为
;则三个函数的导函数分别记为 ,
, ,
, ,由此可以得到
,由此可以得到 ,
, ,
, ,通过推理得到
,通过推理得到 。
。
考点:合情推理、导函数的求法

练习册系列答案
相关题目
设函数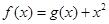 ,曲线
,曲线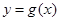 在点
在点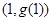 处的切线方程为
处的切线方程为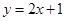 ,则曲线
,则曲线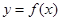 在点
在点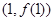 处切线的斜率为
处切线的斜率为
A.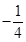 | B. | C.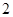 | D.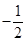 |
函数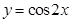 在点
在点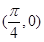 处的切线方程是( )
处的切线方程是( )
A.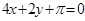 | B.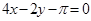 | C.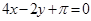 | D.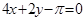 |
设 ,
,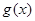 分别是定义在
分别是定义在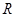 上的奇函数和偶函数,当
上的奇函数和偶函数,当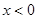 时,
时,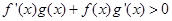 ,且
,且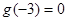 ,则不等式
,则不等式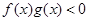 的解集是 ( )
的解集是 ( )
A. | B.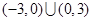 |
C. | D.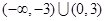 |
若函数 在
在 内为增函数,则实数
内为增函数,则实数 的取值范围是( )
的取值范围是( )
A. | B. | C. | D. |
设 ,
, ,
, ,……,
,……, ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |
曲线 在
在 处的切线的倾斜角是( )
处的切线的倾斜角是( )
A. | B. | C. | D. |
设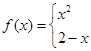
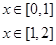 ,则
,则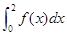 等于( )
等于( )
A.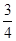 | B.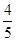 | C.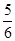 | D.不存在 |
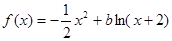 在
在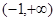 上是减函数,则
上是减函数,则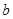 的取值范围是( )
的取值范围是( )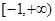

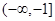
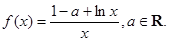 .则有
.则有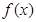 的极大值为________.
的极大值为________.