题目内容
已知集合,对于数列中.
(Ⅰ)若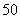 项数列
项数列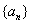 满足
满足 ,
, ,则数列
,则数列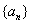 中有多少项取值为零?(
中有多少项取值为零?(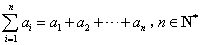 )
)
(Ⅱ)若各项非零数列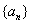 和新数列
和新数列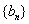 满足
满足 ().
().
(ⅰ)若首项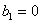 ,末项
,末项 ,求证数列
,求证数列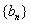 是等差数列;
是等差数列;
(ⅱ)若首项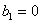 ,末项
,末项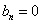 ,记数列
,记数列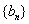 的前
的前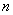 项和为
项和为 ,求
,求 的最大值和最小值.
的最大值和最小值.
解:(Ⅰ)设数列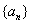 中项为
中项为 分别有
分别有 项.由题意知
项.由题意知
解得 .所以数列
.所以数列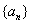 中有
中有 项取值为零.
项取值为零.
(Ⅱ)
(ⅰ) 且
且 ,得到
,得到 ,
,
若 ,则满足
,则满足 .此时
.此时 ,数列
,数列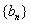 是等差数列;
是等差数列;
若 中有
中有 个
个 ,则
,则 不满足题意;
不满足题意;
所以数列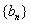 是等差数列.
是等差数列.
(ⅱ)因为数列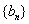 满足
满足 ,所以
,所以 ,
,
根据题意有末项 ,所以
,所以 .
.
而 ,于是
,于是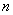 为正奇数,且
为正奇数,且 中有
中有 个
个 和
和 个
个 .
.


要求 的最大值,则只需
的最大值,则只需 前
前 项取
项取 ,后
,后 项取
项取 ,
,
所以 (
(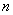 为正奇数).
为正奇数).
要求 的最小值,则只需
的最小值,则只需 前
前 项取
项取 ,后
,后 项取
项取 ,
,
则 (
(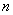 为正奇数).
为正奇数).

练习册系列答案
相关题目
已知函数满足,当时,,若在区间上方程有两个不同的实根,则实数的取值范围是( )
| A. | B. | C. | D. |
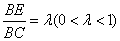 ,则满足
,则满足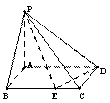
 :
: (
( 为参数)的圆心坐标为__________;直线
为参数)的圆心坐标为__________;直线 :
: 被圆
被圆 .
. 为焦点在
为焦点在 轴上的椭圆,则实数
轴上的椭圆,则实数 ,
, 满足( )
满足( ) (B)
(B) (C)
(C) (D)
(D)
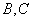 为圆
为圆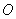 上的两个点,
上的两个点, 为
为 延长线上一点,
延长线上一点, 为圆
为圆 为切点. 若
为切点. 若 ,
, ,则
,则 ______;
______; ______.
______.
 B.
B.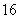 C.
C.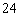 D.
D.