题目内容
等比数列{cn}满足cn+1+cn=10•4n-1,n∈N*,数列{an}满足cn=2an
(1)求{an}的通项公式;
(2)数列{bn}满足bn=
,Tn为数列{bn}的前n项和.求
Tn;
(3)是否存在正整数m,n(1<m<n),使得T1,Tm,Tn成等比数列?若存在,求出所有m,n的值;若不存在,请说明理由.
(1)求{an}的通项公式;
(2)数列{bn}满足bn=
| 1 |
| an•an+1 |
| lim |
| n→∞ |
(3)是否存在正整数m,n(1<m<n),使得T1,Tm,Tn成等比数列?若存在,求出所有m,n的值;若不存在,请说明理由.
(1)由题意可得,c1+c2=10,c2+c3=c1q+c2q=40,
所以公比q=4(2分)
∴c1+4c1=10
∴c1=2(3分)
由等比数列的通项公式可得,cn=2•4n-1=22n-1(4分)
∵cn=2an=22n-1
∴an=2n-1(15分)
(2)∵bn=
=
∴bn=
(
-
)(6分)
于是Tn=
[(1-
)+(
-
)+…+(
-
)]=
(8分)
∴
Tn=
(10分)
(3)假设否存在正整数m,n(1<m<n),使得T1,Tm,Tn成等比数列,
则(
)2=
•
,(12分)
可得
=
>0,
由分子为正,解得1-
<m<1+
,
由m∈N*,m>1,得m=2,此时n=12,
当且仅当m=2,n=12时,T1,Tm,Tn成等比数列. (16分)
说明:只有结论,m=2,n=12时,T1,Tm,Tn成等比数列.若学生没有说明理由,则只能得 13分
所以公比q=4(2分)
∴c1+4c1=10
∴c1=2(3分)
由等比数列的通项公式可得,cn=2•4n-1=22n-1(4分)
∵cn=2an=22n-1
∴an=2n-1(15分)
(2)∵bn=
| 1 |
| an•an+1 |
| 1 |
| (2n-1)(2n+1) |
∴bn=
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
于是Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| n |
| 2n+1 |
∴
| lim |
| n→∞ |
| 1 |
| 2 |
(3)假设否存在正整数m,n(1<m<n),使得T1,Tm,Tn成等比数列,
则(
| m |
| 2m+1 |
| 1 |
| 3 |
| n |
| 2n+1 |
可得
| 3 |
| n |
| -2m2+4m+1 |
| m2 |
由分子为正,解得1-
| ||
| 2 |
| ||
| 2 |
由m∈N*,m>1,得m=2,此时n=12,
当且仅当m=2,n=12时,T1,Tm,Tn成等比数列. (16分)
说明:只有结论,m=2,n=12时,T1,Tm,Tn成等比数列.若学生没有说明理由,则只能得 13分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
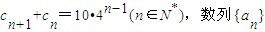 的前n项和为Sn,且an=log2cn.
的前n项和为Sn,且an=log2cn.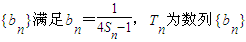 的前n项和,是否存在正整数m,(m>1),使得T1,Tm,T6m成等比数列?若存在,求出所有m的值;若不存在,请说明理由.
的前n项和,是否存在正整数m,(m>1),使得T1,Tm,T6m成等比数列?若存在,求出所有m的值;若不存在,请说明理由.