题目内容
若直线mx-ny=4与⊙O：x2+y2=4没有交点，则过点P（m，n）的直线与椭圆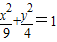
的交点个数是（ ）A．至多为1
B．2
C．1
D．0
【答案】分析：根据直线与圆没有交点得到圆心到直线的距离大于半径列出不等式，化简后得到m2+n2＜4说明P在⊙O的圆内，根据椭圆方程得到短半轴为2，而圆的半径也为2，所以点P在椭圆内部，所以过P的直线与椭圆有两个交点．
解答：解：由题意圆心（0，0）到直线mx-ny=4的距离d=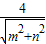
＞2=r，
即m2+n2＜4，点（m，n）在以原点为圆心，2为半径的圆内，
与椭圆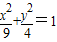
的交点个数为2，
故选B
点评：此题要求学生掌握直线与圆的位置关系，会用点到直线的距离公式化简求值，以及掌握椭圆的简单性质．
解答：解：由题意圆心（0，0）到直线mx-ny=4的距离d=
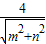＞2=r，即m2+n2＜4，点（m，n）在以原点为圆心，2为半径的圆内，
与椭圆
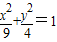的交点个数为2，故选B
点评：此题要求学生掌握直线与圆的位置关系，会用点到直线的距离公式化简求值，以及掌握椭圆的简单性质．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
若直线mx+ny=4和圆x2+y2=4没有公共点，则过点（m，n）的直线与椭圆
+
=1的公共点个数为（ ）
| x2 |
| 9 |
| y2 |
| 4 |
| A、至多一个 | B、0个 |
| C、1个 | D、2个 |
若直线mx+ny=4和圆x2+y2=4没有公共点，则过点（m，n）的直线与椭圆
+
=1的公共点有（ ）
| x2 |
| 16 |
| y2 |
| 4 |
| A、0 个 |
| B、1个 |
| C、2 个 |
| D、最多一个 |