题目内容
判断下列两个试验是否为古典概型,并说明理由.(1)在线段［0,3］上任取一点,求此点的坐标小于1的概率;
(2)从1,2,3,4四个数中任意取出两个数,求所取两数之一是2的概率.
思路分析：根据古典概型的定义及特征进行判断.
解:(1)在线段［0,3］上任取一点,此点可以在［0,3］上的任一位置,且在每个位置的可能性是相同的,具备等可能性.但试验的结果是无限多个,不满足古典概型的条件,即不满足试验结果的有限性.因此不属于古典概型.
(2)此问题属于古典概型,因为此试验的所有基本事件共有6个:{1,2},{1,3},{1,4},{2,3},{2,4},{3,4},且每个事件的出现是等可能的,因此属于古典概型,所取两数之一是2的概率为P=
=
.
点评:判断一个概率模型是否为古典概型,就是看它是否符合古典概型的两个基本特征,即有限性和等可能性.
练习册系列答案
相关题目
下列说法中错误的是（ ）
| A、如果变量x与y之间存在着线性相关关系，则我们根据试验数据得到的点（xi，yi）（i=1，2，…，n）将散布在某一条直线的附近 | ||
| B、如果两个变量x与y之间不存在着线性关系，那么根据它们的一组数据（xi，yi）（i=1，2，…，n）不能写出一个线性方程 | ||
C、设x，y是具有相关关系的两个变量，且x关于y的线性回归方程为
| ||
| D、为使求出的线性回归方程有意义，可用统计检验的方法来判断变量y与x之间是否存在线性相关关系 |
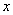与
之间存在着线性相关关系，则我们根据试验数据得到的点
将散布在某一条直线的附近
，
叫做回归系数
与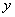
之间存在着线性相关关系，则我们根据试验数据得到的点
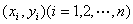将散布在某一条直线的附近
，
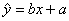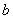叫做回归系数