题目内容
4.某市有A、B两所示范高中响应政府号召,对该市甲、乙两个教育落后地区开展支教活动.经上级研究决定:向甲地派出3名A校教师和2名B校教师,向乙地派出3名A校教师和3名B校教师.由于客观原因,需从拟派往甲、乙两地的教师中各自任选一名互换支教地区,则互换后A校教师派往甲地区人数不少于3名的概率为$\frac{7}{10}$.分析 “甲地区A校教师人数不少于3名”包括两个事件:“甲地区A校教师人数有3名”和“甲地区A校教师人数有4名”,分别求出其概率,由此利用互斥事件概率加法公式能求出甲地区A校教师人数不少于3名的概率.
解答 解:令“甲地区A校教师人数不少于3名”为事件F,
包括两个事件:“甲地区A校教师人数有3名”设为事件F1;
“甲地区A校教师人数有4名”设为事件F2,
则P(F1)=$\frac{{C}_{3}^{1}}{{C}_{5}^{1}}$•$\frac{{C}_{3}^{1}}{{C}_{6}^{1}}$+$\frac{{C}_{2}^{1}}{{C}_{5}^{1}}$•$\frac{{C}_{3}^{1}}{{C}_{6}^{1}}$=$\frac{1}{2}$,P(F2)=$\frac{{C}_{2}^{1}}{{C}_{5}^{1}}$•$\frac{{C}_{3}^{1}}{{C}_{6}^{1}}$=$\frac{1}{5}$,
∴甲地区A校教师人数不少于3名的概率为:
P(F)=P(F1)+P(F2)=$\frac{1}{2}$+$\frac{1}{5}$=$\frac{7}{10}$.
故答案为:$\frac{7}{10}$.
点评 本题考查概率的求法,是中档题,解题时要注意等可能事件概率计算公式、互斥事件概率加法公式的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.已知f(x)是以2为周期的偶函数,当x∈[0,1]时,f(x)=-x,那么在区间[-1,3]上,关于x的方程f(x)=kx+k-1(其中k为不等于1的实数)有四个不同的实数根,则k的取值范围是( )
| A. | ( ) | B. | (0,$\frac{1}{2}$) | C. | (0,$\frac{1}{4}$) | D. | (0,$\frac{1}{3}$) |
19.某市场调查员在同一天对本市的5家商场的某商品的一天销售量及其价格进行调查,5家商场的售价x(元)和销售量y(件)之间的一组数据如下表所示:
由散点图可知,销售量y与价格x之间有较好的线性相关关系,且回归直线方程是$\widehat{y}$=-3.2x+4a,则实数a等于( )
| 价格x(元) | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y(件) | 11 | a | 8 | 6 | 5 |
| A. | 7 | B. | 8.5 | C. | 9 | D. | 10 |
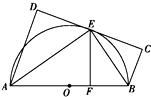 如图,AB为☉O的直径,直线CD与☉O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直AB于F,连接AE,BE.求证:∠FEB=∠CEB.
如图,AB为☉O的直径,直线CD与☉O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直AB于F,连接AE,BE.求证:∠FEB=∠CEB.