题目内容
已知直线l的参数方程为 (t为参数),P是椭圆
(t为参数),P是椭圆 上任意一点,求点P到直线l的距离的最大值.
上任意一点,求点P到直线l的距离的最大值.
解:直线l的参数方程为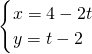 ,(t为参数)故直线l的普通方程为x+2y=0.
,(t为参数)故直线l的普通方程为x+2y=0.
因为P为椭圆 上任意点,故可设 P(2cosθ,sinθ) 其中 θ∈R.
上任意点,故可设 P(2cosθ,sinθ) 其中 θ∈R.
因此点P到直线l的距离是 d= =
= ,故当 θ=kπ+
,故当 θ=kπ+ 时,
时,
d 取得最大值 =
= .
.
分析:把参数方程化为普通方程,求出点P到直线l的距离d= ,令 θ=kπ+
,令 θ=kπ+ ,即得d 的最大值.
,即得d 的最大值.
点评:本题考查把参数方程化为普通方程的方法,点到直线的距离公式的应用,正弦函数的最值.求出点P到直线l的距离d= ,是解题的关键.
,是解题的关键.
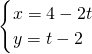 ,(t为参数)故直线l的普通方程为x+2y=0.
,(t为参数)故直线l的普通方程为x+2y=0.因为P为椭圆
 上任意点,故可设 P(2cosθ,sinθ) 其中 θ∈R.
上任意点,故可设 P(2cosθ,sinθ) 其中 θ∈R.因此点P到直线l的距离是 d=
 =
= ,故当 θ=kπ+
,故当 θ=kπ+ 时,
时,d 取得最大值
 =
= .
.分析:把参数方程化为普通方程,求出点P到直线l的距离d=
 ,令 θ=kπ+
,令 θ=kπ+ ,即得d 的最大值.
,即得d 的最大值.点评:本题考查把参数方程化为普通方程的方法,点到直线的距离公式的应用,正弦函数的最值.求出点P到直线l的距离d=
 ,是解题的关键.
,是解题的关键. 
练习册系列答案
相关题目