题目内容
已知△ABC中,A(0,1),B(2,4)C(6,1),P为平面上任意一点,M、N分别使 ,
, ,给出下列相关命题:①
,给出下列相关命题:① ;②直线MN的方程为3x+10y-28=0;③直线MN必过△ABC的外心;④向量
;②直线MN的方程为3x+10y-28=0;③直线MN必过△ABC的外心;④向量 所在射线必过N点,上述四个命题中正确的是 .(将正确的选项全填上).
所在射线必过N点,上述四个命题中正确的是 .(将正确的选项全填上).
【答案】分析:设P(x,y),M(x1,y1),N(x2,y2),由题设条件求出M(1, ).N(
).N( ).由此能够得到
).由此能够得到 与
与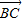 不平行;直线MN的方程为3x+10y-28=0;直线MN不过△ABC的外心;向量
不平行;直线MN的方程为3x+10y-28=0;直线MN不过△ABC的外心;向量 所在射线不一定过N点.
所在射线不一定过N点.
解答:解:设P(x,y),M(x1,y1),N(x2,y2),
∵A(0,1),B(2,4)C(6,1),
∴ ,
, ,
, ,
, ,
, ,
,
∵ ,
,
∴(x1-x,y1-y)= =(1-x,
=(1-x, ),
),
∴M(1, ).
).
∵ ,
,
∴( )=
)= (8-3x,6-3y)=(
(8-3x,6-3y)=( ,2-y),
,2-y),
∴N( ).
).
∴ ,
,
∵ ,
, =-3≠0,
=-3≠0,
∴ 与
与 不平行,
不平行,
故①不正确;
∵M(1, ),N(
),N( ),
),
∴直线MN的方程为 ,
,
整理,得3x+10y-28=0,
故②正确;
∵A(0,1),B(2,4)C(6,1),
∴ ,线段AB的中点(1,
,线段AB的中点(1, ),kAC=0,线段AC的中点(3,1),
),kAC=0,线段AC的中点(3,1),
∴线段AB的中垂线为:y- =-
=- ,即4x+6y-19=0,
,即4x+6y-19=0,
线段AC的中垂线为x=3,
解方程组 ,得△ABC的外心为(3,
,得△ABC的外心为(3, ),
),
把(3, )代入3x+10y-28=0,不成立,
)代入3x+10y-28=0,不成立,
∴直线MN不过△ABC的外心,故③不正确;
∵A(0,1),B(2,4)C(6,1),
∴λ( )=λ[(2,3)+(6,0)]=λ(8,3)=(8λ,3λ),
)=λ[(2,3)+(6,0)]=λ(8,3)=(8λ,3λ),
∴向量 所在射线不一定过N点,故④不正确.
所在射线不一定过N点,故④不正确.
故答案为:②.
点评:本题考查命题的真假判断与应用,综合性强,难度大.解题时要认真审题,仔细解答,注意等价转化思想的合理运用.
 ).N(
).N( ).由此能够得到
).由此能够得到 与
与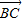 不平行;直线MN的方程为3x+10y-28=0;直线MN不过△ABC的外心;向量
不平行;直线MN的方程为3x+10y-28=0;直线MN不过△ABC的外心;向量 所在射线不一定过N点.
所在射线不一定过N点.解答:解:设P(x,y),M(x1,y1),N(x2,y2),
∵A(0,1),B(2,4)C(6,1),
∴
 ,
, ,
, ,
, ,
, ,
,∵
 ,
,∴(x1-x,y1-y)=
 =(1-x,
=(1-x, ),
),∴M(1,
 ).
).∵
 ,
,∴(
 )=
)= (8-3x,6-3y)=(
(8-3x,6-3y)=( ,2-y),
,2-y),∴N(
 ).
).∴
 ,
,∵
 ,
, =-3≠0,
=-3≠0,∴
 与
与 不平行,
不平行,故①不正确;
∵M(1,
 ),N(
),N( ),
),∴直线MN的方程为
 ,
,整理,得3x+10y-28=0,
故②正确;
∵A(0,1),B(2,4)C(6,1),
∴
 ,线段AB的中点(1,
,线段AB的中点(1, ),kAC=0,线段AC的中点(3,1),
),kAC=0,线段AC的中点(3,1),∴线段AB的中垂线为:y-
 =-
=- ,即4x+6y-19=0,
,即4x+6y-19=0,线段AC的中垂线为x=3,
解方程组
 ,得△ABC的外心为(3,
,得△ABC的外心为(3, ),
),把(3,
 )代入3x+10y-28=0,不成立,
)代入3x+10y-28=0,不成立,∴直线MN不过△ABC的外心,故③不正确;
∵A(0,1),B(2,4)C(6,1),
∴λ(
 )=λ[(2,3)+(6,0)]=λ(8,3)=(8λ,3λ),
)=λ[(2,3)+(6,0)]=λ(8,3)=(8λ,3λ),∴向量
 所在射线不一定过N点,故④不正确.
所在射线不一定过N点,故④不正确.故答案为:②.
点评:本题考查命题的真假判断与应用,综合性强,难度大.解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目