题目内容
已知向量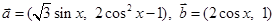 ,且函数
,且函数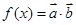 .
.
(1) 求函数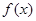 在区间
在区间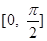 上的最大值和最小值;
上的最大值和最小值;
(2) 求函数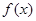 的单调减区间.
的单调减区间.
【答案】
(1)最大值为2,最小值为 ;(2)
;(2) .
.
【解析】第一问中,首先利用向量的数量积公式化简 ,所以
,所以 ,然后分析
,然后分析 ,从而得到
,从而得到
∴ 的最大值为2,最小值为
的最大值为2,最小值为
第二问中,根据第一问中的结论, ,所以
,所以 的单调递减区间为
的单调递减区间为 得到结论。
得到结论。
解:(1) ----------2分
----------2分
令 ,∴
,∴
∴ 的最大值为2,最小值为
的最大值为2,最小值为 -------6分
-------6分
(2) -----------9分
-----------9分
∴ 的单调递减区间为
的单调递减区间为 ------------12分
------------12分

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,且函数
,且函数 •
•
 个单位得到函数g(x),求函数g(x)的单调递增区间.
个单位得到函数g(x),求函数g(x)的单调递增区间. ,且函数
,且函数 •
•
 个单位得到函数g(x),求函数g(x)的单调递增区间.
个单位得到函数g(x),求函数g(x)的单调递增区间. ,
, ,函数f(x)=
,函数f(x)= .
.