题目内容
下列命题错误的是
- A.对于等比数列{an}而言,若m+n=k+S,m、n、k、S∈N*,则有am•an=ak•aS
- B.点(-
 ,0)为函数f(x)=tan(2x+
,0)为函数f(x)=tan(2x+ )的一个对称中心
)的一个对称中心 - C.若|
 |=1,|
|=1,| |=2,向量
|=2,向量 与向量
与向量 的夹角为120°,则
的夹角为120°,则 在向量
在向量 上的投影为1
上的投影为1 - D.“sinα=sinβ”的充要条件是“α+β=(2k+1)π或α-β=2kπ (k∈Z)”
C
分析:由等比数列通项公式,能推导出A正确;f(x)=tan(2x+ )的对称中心是(
)的对称中心是(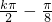 ,0),k∈Z;由|
,0),k∈Z;由| |=1,|
|=1,| |=2,向量
|=2,向量 与向量
与向量 的夹角为120°,知向量
的夹角为120°,知向量 在向量
在向量 上的投影为:
上的投影为: =2×
=2× =-1,故C不对;;“sinα=sinβ”?“α+β=(2k+1)π或α-β=2kπ (k∈Z.
=-1,故C不对;;“sinα=sinβ”?“α+β=(2k+1)π或α-β=2kπ (k∈Z.
解答:由等比数列通项公式,能推导出A正确;
f(x)=tan(2x+ )的对称中心是(
)的对称中心是(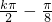 ,0),k∈Z,故B成立;
,0),k∈Z,故B成立;
∵| |=1,|
|=1,| |=2,向量
|=2,向量 与向量
与向量 的夹角为120°,
的夹角为120°,
∴向量 在向量
在向量 上的投影为:
上的投影为: =2×
=2× =-1,故C不对;
=-1,故C不对;
“sinα=sinβ”?“α+β=(2k+1)π或α-β=2kπ (k∈Z)”,故D正确.
故选C.
点评:本题考查命题的真假判断,是基础题.解题时要认真审题,注意等比数列、三角函数、平面向量等知识点的灵活运用.
分析:由等比数列通项公式,能推导出A正确;f(x)=tan(2x+
 )的对称中心是(
)的对称中心是(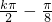 ,0),k∈Z;由|
,0),k∈Z;由| |=1,|
|=1,| |=2,向量
|=2,向量 与向量
与向量 的夹角为120°,知向量
的夹角为120°,知向量 在向量
在向量 上的投影为:
上的投影为: =2×
=2× =-1,故C不对;;“sinα=sinβ”?“α+β=(2k+1)π或α-β=2kπ (k∈Z.
=-1,故C不对;;“sinα=sinβ”?“α+β=(2k+1)π或α-β=2kπ (k∈Z.解答:由等比数列通项公式,能推导出A正确;
f(x)=tan(2x+
 )的对称中心是(
)的对称中心是(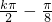 ,0),k∈Z,故B成立;
,0),k∈Z,故B成立;∵|
 |=1,|
|=1,| |=2,向量
|=2,向量 与向量
与向量 的夹角为120°,
的夹角为120°,∴向量
 在向量
在向量 上的投影为:
上的投影为: =2×
=2× =-1,故C不对;
=-1,故C不对;“sinα=sinβ”?“α+β=(2k+1)π或α-β=2kπ (k∈Z)”,故D正确.
故选C.
点评:本题考查命题的真假判断,是基础题.解题时要认真审题,注意等比数列、三角函数、平面向量等知识点的灵活运用.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案
相关题目
 是两不同直线,
是两不同直线, 是两不同平面,则下列命题错误的是
是两不同平面,则下列命题错误的是 ,
, ∥
∥ ,则
,则
 ,
, ,则
,则 ∥
∥ ,则
,则
 ,
, 为实数,且
为实数,且 ,则下列命题错误的是
,则下列命题错误的是 ,
, ,则
,则 B.若
B.若 ,则
,则 D.若
D.若 ,则
,则 “的逆否命题为”若
“的逆否命题为”若
 ,则
,则
 为假命题,则
为假命题,则 ,
, 均为假命题
均为假命题 的充分不必要条件
的充分不必要条件
 ”是正确的
”是正确的 是假命题,则
是假命题,则 均为假命题
均为假命题 ”是“
”是“ ”的充分不必要条件
”的充分不必要条件 N*,均有S n>0
N*,均有S n>0