题目内容
已知函数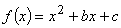 对任意
对任意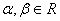 都有
都有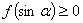 ,且
,且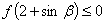 .
.
(1)求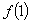 的值;
的值;
(2)求证: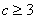 .
.
(3)若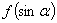 的最大值为10,求
的最大值为10,求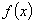 的表达式.
的表达式.
(1)因为 .
.
且对任意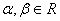 都有
都有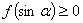 ,且
,且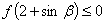 .
.
所以对 ,对
,对 .
.
于是 .
.
(2)由于对 ,对
,对 ,
,
所以二次函数的对称轴满足: ,所以
,所以 .
.
由(1)知, ,所以
,所以 ,于是
,于是 .
.
(3)因为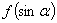 的最大值为10,所以
的最大值为10,所以 在
在 的最大值为10,
的最大值为10,
又因为二次函数开口向上且对称轴满足: ,所以
,所以 在
在 单调递减,所以
单调递减,所以 ,于是
,于是 .又由(1)知,
.又由(1)知, ,所以
,所以
联立解得 , 所以
, 所以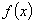 的表达式为
的表达式为 .
.

练习册系列答案
相关题目


 满足
满足 ,
, ,则
,则 的前10项和等于( )
的前10项和等于( ) B.
B.  C.
C. D.
D.
 中,
中, ,
, 是
是 上一点,且
上一点,且 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
 ,
, ,若
,若 ,则实数
,则实数 ________.
________. ,且
,且 ,
, ,则实数
,则实数 的取值范围是 .
的取值范围是 . 满足
满足 ,则
,则 的最大值为 .
的最大值为 .
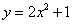 中的
中的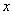 ,
,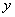 是具有相关关系的两个变量
是具有相关关系的两个变量