题目内容
设正方体的棱长为
,则它的外接球的表面积为
2
| ||
| 3 |
4π
4π
.分析:棱长为
的正方体的外接球之间一个重要的几何特征是此正方体的体对角线恰好是外接球的直径,由此先求出体对角线,即得球的直径,再由表面积公式求出球的表面积即可
2
| ||
| 3 |
解答:解:由题意知正方体的体对角线长度是
×
=2,故球体的直径是2,半径是1
故球的表面积是4×π×12=4π,
故答案为:4π
| 3 |
2
| ||
| 3 |
故球的表面积是4×π×12=4π,
故答案为:4π
点评:本题考查球的体积与表面积,求解本题,关键是两个几何体的共同特征求出球的直径以及根据球的面积公式求面积,本题考查了空间想像能力以及转化化归的思想.

练习册系列答案
相关题目
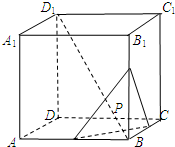 如图,正方体ABCD-A1B1C1D1的棱长为2
如图,正方体ABCD-A1B1C1D1的棱长为2