题目内容
在△ABC中,角A,B,C所对的边分别为a,b,c,且满足csinA=acosC.(1)求角C的大小;
(2)求
 sinA-cos(B+
sinA-cos(B+ )的最大值,并求取得最大值时角A、B的大小.
)的最大值,并求取得最大值时角A、B的大小.
【答案】分析:(1)利用正弦定理化简csinA=acosC.求出tanC=1,得到C=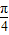 .
.
(2)B=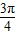 -A,化简
-A,化简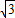 sinA-cos (B+
sinA-cos (B+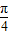 )=2sin(A+
)=2sin(A+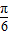 ).因为0<A<
).因为0<A<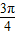 ,推出
,推出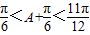
求出2sin(A+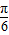 )取得最大值2.得到A=
)取得最大值2.得到A=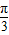 ,B=
,B=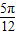
解答:解:(1)由正弦定理得 sinCsinA=sinAcosC,
因为0<A<π,所以sinA>0.从而sinC=cosC,
又cosC≠0,所以tanC=1,C=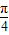 .
.
(2)有(1)知,B=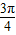 -A,于是
-A,于是
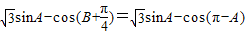
=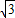 sinA+cosA
sinA+cosA
=2sin(A+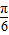 ).
).
因为0<A<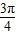 ,所以
,所以
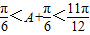
从而当A+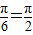 ,即A=
,即A=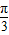 时
时
2sin(A+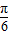 )取得最大值2.
)取得最大值2.
综上所述,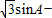 cos (B+
cos (B+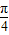 )的最大值为2,此时A=
)的最大值为2,此时A=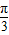 ,B=
,B=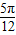
点评:本题是中档题,考查三角形的有关知识,正弦定理的应用,三角函数的最值,常考题型.
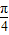 .
.(2)B=
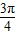 -A,化简
-A,化简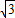 sinA-cos (B+
sinA-cos (B+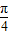 )=2sin(A+
)=2sin(A+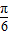 ).因为0<A<
).因为0<A<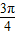 ,推出
,推出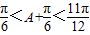
求出2sin(A+
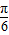 )取得最大值2.得到A=
)取得最大值2.得到A=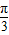 ,B=
,B=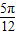
解答:解:(1)由正弦定理得 sinCsinA=sinAcosC,
因为0<A<π,所以sinA>0.从而sinC=cosC,
又cosC≠0,所以tanC=1,C=
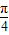 .
.(2)有(1)知,B=
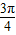 -A,于是
-A,于是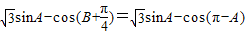
=
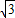 sinA+cosA
sinA+cosA=2sin(A+
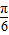 ).
).因为0<A<
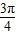 ,所以
,所以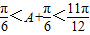
从而当A+
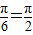 ,即A=
,即A=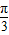 时
时2sin(A+
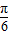 )取得最大值2.
)取得最大值2.综上所述,
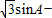 cos (B+
cos (B+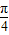 )的最大值为2,此时A=
)的最大值为2,此时A=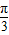 ,B=
,B=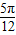
点评:本题是中档题,考查三角形的有关知识,正弦定理的应用,三角函数的最值,常考题型.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a,b,c,若b2+c2-a2=
bc,且b=
a,则下列关系一定不成立的是( )
| 3 |
| 3 |
| A、a=c |
| B、b=c |
| C、2a=c |
| D、a2+b2=c2 |