题目内容

中心在原点，焦点在x轴上，若长轴的长为18，且两个焦点恰好将长轴三等分，则此椭圆方程为________．


分析：根据题意，2a=18，且2c=•2a=6，可得a=9且c=3，再根据椭圆中a、b、c的平方关系得到b2的值，结合椭圆焦点在x轴，得到此椭圆的标准方程．
解答：椭圆长轴的长为18，即2a=18，得a=9
∵两个焦点恰好将长轴三等分，
∴2c=•2a=6，得c=3
因此，b2=a2-c2=81-9=72，再结合椭圆焦点在x轴上，
可得此椭圆方程为
故答案为：
点评：本题给出椭圆的长轴长和焦点的位置，求椭圆的标准方程，着重考查了椭圆的基本概念和标准方程等知识，属于基础题．
练习册系列答案
相关题目
已知椭圆w的中心在原点，焦点在x轴上，长轴长为4，离心率为
6
3
，△ABC的顶点A，B在椭圆w上，C在直线l：y=x+2上，且AB∥l．
（1）求椭圆w的方程；
（2）当AB边通过坐标原点O时，求AB的长及△ABC的面积；
（3）当∠ABC=90°，且斜边AC的长最大时，求AB所在直线的方程．
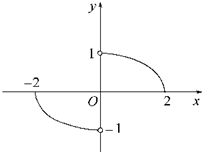精英家教网如图，函数y=f（x）的图象是中心在原点、焦点在x轴上的椭圆的两段弧，则不等式f（x）＜f（-x）+x的解集为（　　）
A、{x|-
2
＜x＜0或
2
＜x≤2}
B、{x|-2≤x＜-
2
或
2
＜x≤2}
C、{x|-2≤x＜-
2
2
或
2
2
＜x≤2}
D、{x|-
2
＜x＜
2
，且x≠0}
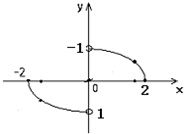精英家教网如图，函数y=f（x）的图象是中心在原点，焦点在x轴上的椭圆的两段弧，则不等式f（x）＜f（-x）+x的解集为（　　）
A、{
2
2
＜x≤2或
2
2
＜x≤2}
B、{x|-2≤x＜
2
或
2
＜x≤2}
C、{x|-
2
＜x＜0或
2
＜x≤2}
D、{x|-
2
＜x＜
2
，且x≠0}

（12分）

    已知椭圆中心在原点，焦点在x轴上，长轴长等于12，离心率为.

（Ⅰ）求椭圆的标准方程；

（Ⅱ）过椭圆左顶点作直线l垂直于x轴，若动点M到椭圆右焦点的距离比它到直线l的距离小4，求点M的轨迹方程.

 
已知椭圆w的中心在原点，焦点在x轴上，长轴长为4，离心率为
6
3
，△ABC的顶点A，B在椭圆w上，C在直线l：y=x+2上，且AB∥l．
（1）求椭圆w的方程；
（2）当AB边通过坐标原点O时，求AB的长及△ABC的面积；
（3）当∠ABC=90°，且斜边AC的长最大时，求AB所在直线的方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网