题目内容
某校高二年级研究性学习小组,为了分析2011年我国宏观经济形势,上网查阅了2010年和2011年2-6月我国CPI同比(即当年某月与前一年同月相比)的增长数据(见下表),但2011年4,5,6三个月的数据(分别记为x,y,z)没有查到.有的同学清楚记得2011年2,3,4,5,6五个月的CPI数据成等差数列.(1)求x,y,z的值;
(2)求2011年2-6月我国CPI的数据的方差;
(3)一般认为,某月CPI达到或超过3个百分点就已经通货膨胀,而达到或超过5个百分点则严重通货膨胀.现随机地从上表2010年的五个月和2011年的五个月的数据中各抽取一个数据,求相同月份2010年通货膨胀,并且2011年严重通货膨胀的概率.
附表:我国2010年和2011年2~6月的CPI数据(单位:百分点.注:1个百分点=1%)
| 年份 | 二月 | 三月 | 四月 | 五月 | 六月 |
| 2010 | 2.7 | 2.4 | 2.8 | 3.1 | 2.9 |
| 2011 | 4.9 | 5.0 | x | y | z |
【答案】分析:(1)根据题意,结合等差数列的性质,可得该数列的公差为0.1,进而可得x、y、z的值;
(2)由(1)的结论可得2011年中2-6月全部数据,先计算出5个数据的平均数,进而由方差公式计算可得答案;
(3)根据题意,用m表示2010年的数据,n表示2011年的数据,则(m,n)表示随机地从2010年的五个月和2011年的五个月的数据中各抽取一个数据的基本事件,由列举法可得抽取数据的情况,分析可得事件“相同月份2010年通货膨胀,并且2011年严重通货膨胀”包含的基本事件的数目,由古典概型公式,计算可得答案.
解答:解:(1)依题意得4.9,5.0,x,y,z成等差数列,所以公差d=5.0-4.9=0.1,
故x=5.0+0.1=5.1,y=x+0.1=5.2,z=y+0.1=5.3;
(2)由(1)知2011年2~6月我国CPI的数据为:4.9,5.0,5.1,5.2,5.3
其平均数为: ,
,
其方差为: =0.01;
=0.01;
(3)根据题意,用m表示2010年的数据,n表示2011年的数据,则(m,n)表示随机地从2010年的五个月和2011年的五个月的数据中各抽取一个数据的基本事件,
则所有基本事件有:(2.7,4.9),(2.7,5.0),(2.7,5.1),(2.7,5.2),(2.7,5.3),
(2.4,4.9),(2.4,5.0),(2.4,5.1),(2.4,5.2),(2.4,5.3),
(2.8,4.9),(2.8,5.0),(2.8,5.1),(2.8,5.2),(2.8,5.3),
(3.1,4.9),(3.1,5.0),(3.1,5.1),(3.1,5.2),(3.1,5.3),
(2.9,4.9),(2.9,5.0),(2.9,5.1),(2.9,5.2),(2.9,5.3);共25个基本事件;
其中满足相同月份2010年通货膨胀,并且2011年严重通货膨胀的基本事件有(3.1,5.2),有1个基本事件;
所以P= ,即相同月份2010年通货膨胀,并且2011年严重通货膨胀的概率为0.04.
,即相同月份2010年通货膨胀,并且2011年严重通货膨胀的概率为0.04.
点评:本题考查古典概型的计算,涉及等差数列的性质、平均数、方差的计算与列举法的应用,是基础题;注意在列举时做到不重不漏,同时要正确计算.
(2)由(1)的结论可得2011年中2-6月全部数据,先计算出5个数据的平均数,进而由方差公式计算可得答案;
(3)根据题意,用m表示2010年的数据,n表示2011年的数据,则(m,n)表示随机地从2010年的五个月和2011年的五个月的数据中各抽取一个数据的基本事件,由列举法可得抽取数据的情况,分析可得事件“相同月份2010年通货膨胀,并且2011年严重通货膨胀”包含的基本事件的数目,由古典概型公式,计算可得答案.
解答:解:(1)依题意得4.9,5.0,x,y,z成等差数列,所以公差d=5.0-4.9=0.1,
故x=5.0+0.1=5.1,y=x+0.1=5.2,z=y+0.1=5.3;
(2)由(1)知2011年2~6月我国CPI的数据为:4.9,5.0,5.1,5.2,5.3
其平均数为:
 ,
,其方差为:
 =0.01;
=0.01;(3)根据题意,用m表示2010年的数据,n表示2011年的数据,则(m,n)表示随机地从2010年的五个月和2011年的五个月的数据中各抽取一个数据的基本事件,
则所有基本事件有:(2.7,4.9),(2.7,5.0),(2.7,5.1),(2.7,5.2),(2.7,5.3),
(2.4,4.9),(2.4,5.0),(2.4,5.1),(2.4,5.2),(2.4,5.3),
(2.8,4.9),(2.8,5.0),(2.8,5.1),(2.8,5.2),(2.8,5.3),
(3.1,4.9),(3.1,5.0),(3.1,5.1),(3.1,5.2),(3.1,5.3),
(2.9,4.9),(2.9,5.0),(2.9,5.1),(2.9,5.2),(2.9,5.3);共25个基本事件;
其中满足相同月份2010年通货膨胀,并且2011年严重通货膨胀的基本事件有(3.1,5.2),有1个基本事件;
所以P=
 ,即相同月份2010年通货膨胀,并且2011年严重通货膨胀的概率为0.04.
,即相同月份2010年通货膨胀,并且2011年严重通货膨胀的概率为0.04.点评:本题考查古典概型的计算,涉及等差数列的性质、平均数、方差的计算与列举法的应用,是基础题;注意在列举时做到不重不漏,同时要正确计算.

练习册系列答案
相关题目
为了拓展网络市场,腾讯公司为 用户推出了多款
用户推出了多款 应用,如“
应用,如“ 农场”、“
农场”、“ 音乐”、“
音乐”、“ 读书”等.某校研究性学习小组准备举行一次“
读书”等.某校研究性学习小组准备举行一次“ 使用情况”调查,从高二年级的一、二、三、四班中抽取10名学生代表参加,抽取不同班级的学生人数如下表所示:[来源:学#科#网Z#X#X#K]
使用情况”调查,从高二年级的一、二、三、四班中抽取10名学生代表参加,抽取不同班级的学生人数如下表所示:[来源:学#科#网Z#X#X#K]
|
班级 |
一班 |
二班 |
三班 |
四班 |
|
人数 |
2人 |
3人 |
4人 |
1人 |
(1)从这10名学生中随机选出2名,求这2人来自相同班级的概率;
(2) 假设在某时段,三名学生代表甲、乙、丙准备分别从 农场、
农场、 音乐、
音乐、 读书中任意选择一项,他们选择
读书中任意选择一项,他们选择 农场的概率都为
农场的概率都为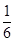 ;选择
;选择 音乐的概率都为
音乐的概率都为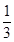 ;选择
;选择 读书的概率都为
读书的概率都为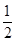 ;他们的选择相互独立.设在该时段这三名学生中选择
;他们的选择相互独立.设在该时段这三名学生中选择 读书的总人数为随机变量
读书的总人数为随机变量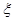 ,求随机变量
,求随机变量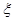 的分布列及数学期望
的分布列及数学期望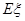 .
.
为了拓展网络市场,腾讯公司为 用户推出了多款
用户推出了多款 应用,如“
应用,如“ 农场”、“
农场”、“ 音乐”、“
音乐”、“ 读书”等.某校研究性学习小组准备举行一次“
读书”等.某校研究性学习小组准备举行一次“ 使用情况”调查,从高二年级的一、二、三、四班中抽取10名学生代表参加,抽取不同班级的学生人数如下表所示:[来源:学#科#网Z#X#X#K]
使用情况”调查,从高二年级的一、二、三、四班中抽取10名学生代表参加,抽取不同班级的学生人数如下表所示:[来源:学#科#网Z#X#X#K]
|
班级 |
一班 |
二班 |
三班 |
四班 |
|
人数 |
2人 |
3人 |
4人 |
1人 |
(1)从这10名学生中随机选出2名,求这2人来自相同班级的概率;
(2) 假设在某时段,三名学生代表甲、乙、丙准备分别从 农场、
农场、 音乐、
音乐、 读书中任意选择一项,他们选择
读书中任意选择一项,他们选择 农场的概率都为
农场的概率都为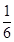 ;选择
;选择 音乐的概率都为
音乐的概率都为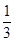 ;选择
;选择 读书的概率都为
读书的概率都为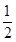 ;他们的选择相互独立.设在该时段这三名学生中选择
;他们的选择相互独立.设在该时段这三名学生中选择 读书的总人数为随机变量
读书的总人数为随机变量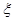 ,求随机变量
,求随机变量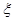 的分布列及数学期望
的分布列及数学期望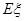 .
.