题目内容
若向量
=(sin(α+
),1),
=(4,4cosα-
),且
⊥
,则sin(α+
)等于
| a |
| π |
| 6 |
| b |
| 3 |
| a |
| b |
| 4π |
| 3 |
-
| 1 |
| 4 |
-
.| 1 |
| 4 |
分析:利用向量垂直的坐标运算可求得sin(α+
)=
,再利用诱导公式即可求得sin(α+
).
| π |
| 3 |
| 1 |
| 4 |
| 4π |
| 3 |
解答:解:∵向量
=(sin(α+
),1),
=(4,4cosα-
),且
⊥
,
∴4sin(α+
)+4cosα-
=0,
∴4(
sinα+
cosα)+)+4cosα=
,
∴2
sinα+6cosα=
,
∴4
(
sinα+
cosα)=
,
∴sin(α+
)=
,
∴sin(α+
)=sin[(α+
)+π]=-sin(α+
)=-
,
故答案为:-
.
| a |
| π |
| 6 |
| b |
| 3 |
| a |
| b |
∴4sin(α+
| π |
| 6 |
| 3 |
∴4(
| ||
| 2 |
| 1 |
| 2 |
| 3 |
∴2
| 3 |
| 3 |
∴4
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∴sin(α+
| π |
| 3 |
| 1 |
| 4 |
∴sin(α+
| 4π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 1 |
| 4 |
故答案为:-
| 1 |
| 4 |
点评:本题考查数量积判断两个平面向量的垂直关系,考查两角和与差的正弦函数及诱导公式,属于中档题.

练习册系列答案
相关题目
若向量a=(cos?,sin?),b=(cos?,sin?), 则a与b一定满足 ( )
则a与b一定满足 ( )
| A.a与b的夹角等于?-? | B.(a+b)⊥(a-b) |
| C.a∥b | D.a⊥b |
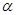 ,sin
,sin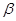 ),b=(cos
),b=(cos