题目内容
若点A的坐标为（3，2），F为抛物线y2=2x的焦点，点p是抛物线上一动点，则|PA|+|PF|取得最小值时点P的坐标是（ ）A.（0,0）?
B.（1,1）?
C.（2,2）?
D.（
,1）?
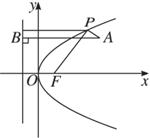
思路分析：∵|PF|等于P点到准线的距离，A在抛物线内部，?
∴|PA|+|PF|的最小值是由A点向抛物线的准线x=-
作垂线（垂足为B）时垂线段AB的长度.
∴|PA|+|PF|最小时，点P的纵坐标为2，从而得点P的横坐标为2.?
∴点P的坐标为（2，2）.?
答案：C
温馨提示
本题根据抛物线定义，利用数形结合思想简捷地得到答案.
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
若点A的坐标为（3，2），F是抛物线y2=2x的焦点，点M在抛物线上移动时，使|MF|+|MA|取得最小值的M的坐标为（ ）
| A、（0，0） | ||
B、(
| ||
C、(1，
| ||
| D、（2，2） |