题目内容
已知函数f(x)=-![]() (x>0),数列{an}中,a1=1,
(x>0),数列{an}中,a1=1,![]() =-f(an),求数列{an}的通项公式.
=-f(an),求数列{an}的通项公式.
an=![]() .
.
解析:
∵![]() =-f(an),
=-f(an),
∴![]() =-
=-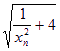 .
.
∴![]() =
=![]() +4.
+4.
∴![]() -
-![]() =4.
=4.
则{![]() }是以
}是以![]() =1为首项,4为公差的等差数列.
=1为首项,4为公差的等差数列.
∴![]() =1+4(n-1)=4n-3.
=1+4(n-1)=4n-3.
∴an2=![]() .
.
∵an>0,
∴an=![]() .
.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|
题目内容
已知函数f(x)=-![]() (x>0),数列{an}中,a1=1,
(x>0),数列{an}中,a1=1,![]() =-f(an),求数列{an}的通项公式.
=-f(an),求数列{an}的通项公式.
an=![]() .
.
∵![]() =-f(an),
=-f(an),
∴![]() =-
=-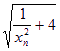 .
.
∴![]() =
=![]() +4.
+4.
∴![]() -
-![]() =4.
=4.
则{![]() }是以
}是以![]() =1为首项,4为公差的等差数列.
=1为首项,4为公差的等差数列.
∴![]() =1+4(n-1)=4n-3.
=1+4(n-1)=4n-3.
∴an2=![]() .
.
∵an>0,
∴an=![]() .
.

 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案 已知函数f(x)=
已知函数f(x)=
|
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、[
|