题目内容
若函数 的定义域和值域均为[1,b](b>1),求a,b的值.
的定义域和值域均为[1,b](b>1),求a,b的值.
解:由函数 ,得对称轴方程是x=1
,得对称轴方程是x=1
故函数在[1,b]上是增函数
又函数 的定义域和值域均为[1,b](b>1),
的定义域和值域均为[1,b](b>1),
故有 ,即
,即 即
即
又b>1,故有
符合题设条件的a,b的值为 .
.
分析:由二次函数的性质知,其对称轴是x=1,由此知函数在[1,b]是一个增函数,由题设条件定义域和值域均为[1,b](b>1),即可转化出关于a,b的方程,求解即可.
点评:本题的考点是二次函数的性质,考查利用二次函数的单调性转化不等式求参数,此类题是函数单调性运用的一个常见题型,本题有可能因不严谨致错,如解题中忘记考虑b>1这一条件,致使出现二个结果.
 ,得对称轴方程是x=1
,得对称轴方程是x=1故函数在[1,b]上是增函数
又函数
 的定义域和值域均为[1,b](b>1),
的定义域和值域均为[1,b](b>1),故有
 ,即
,即 即
即
又b>1,故有

符合题设条件的a,b的值为
 .
.分析:由二次函数的性质知,其对称轴是x=1,由此知函数在[1,b]是一个增函数,由题设条件定义域和值域均为[1,b](b>1),即可转化出关于a,b的方程,求解即可.
点评:本题的考点是二次函数的性质,考查利用二次函数的单调性转化不等式求参数,此类题是函数单调性运用的一个常见题型,本题有可能因不严谨致错,如解题中忘记考虑b>1这一条件,致使出现二个结果.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 的定义域和值域均为
的定义域和值域均为 ,则
,则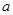 的范围是________.
的范围是________. 的定义域和值域都是[0,1],则a=( )
的定义域和值域都是[0,1],则a=( ) C.
C. D.
D.
 的定义域和值域都是
的定义域和值域都是 ,则实数
,则实数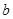 的值为 ( )
的值为 ( )