题目内容
从某学校的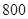 名男生中随机抽取
名男生中随机抽取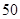 名测量身高,被测学生身高全部介于
名测量身高,被测学生身高全部介于 cm和
cm和 cm之间,将测量结果按如下方式分成八组:第一组[
cm之间,将测量结果按如下方式分成八组:第一组[ ,
, ),第二组[
),第二组[ ,
,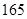 ),…,第八组[
),…,第八组[ ,
, ],右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为
],右图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为 人.
人.
(Ⅰ)求第七组的频率;
(Ⅱ)估计该校的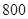 名男生的身高的中位数以及身高在
名男生的身高的中位数以及身高在 cm以上(含
cm以上(含 cm)的人数;
cm)的人数;
(Ⅲ)若从身高属于第六组和第八组的所有男生中随机抽取两名男生,记他们的身高分别为 ,事件
,事件 {
{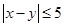 },事件
},事件 {
{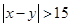 },求
},求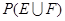 .
.
(1) ,144
,144
(2))
解析试题分析:(Ⅰ)第六组的频率为 ,所以第七组的频率为
,所以第七组的频率为 ; 4分
; 4分
(Ⅱ)身高在第一组[155,160)的频率为 ,
,
身高在第二组[160,165)的频率为 ,
,
身高在第三组[165,170)的频率为 ,
,
身高在第四组[170,175)的频率为 ,
,
由于 ,
,
估计这所学校的800名男生的身高的中位数为 ,则
,则
由 得
得
所以可估计这所学校的800名男生的身高的中位数为 6分
6分
由直方图得后三组频率为 ,
,
所以身高在180cm以上(含180cm)的人数为 人. 8分
人. 8分
(Ⅲ)第六组 的人数为4人,设为
的人数为4人,设为 ,第八组[190,195]的人数为2人, 设为
,第八组[190,195]的人数为2人, 设为 ,则有
,则有
 共15种情况,
共15种情况,
因事件 {
{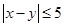 }发生当且仅当随机抽取的两名男生在同一组,所以事件
}发生当且仅当随机抽取的两名男生在同一组,所以事件 包含的基本事件为
包含的基本事件为 共7种情况,故
共7种情况,故 . 10分
. 10分
由于 ,所以事件
,所以事件 {
{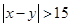 }是不可能事件,
}是不可能事件,
由于事件 和事件
和事件 是互斥事件,所以
是互斥事件,所以 12分
12分
考点:概率与频率
点评:主要是考查了频率与概率以及互斥事件的概率和的运用,属于中档题。

为预防H7N9病毒爆发,某生物技术公司研制出一种H7N9病毒疫苗,为测试该疫苗的有效性(若疫苗有效的概率小于90%,则认为测试没有通过),公司选定2000个样本分成三组,测试结果如下表:
| 分组 | A组 | B组 | C组 |
| 疫苗有效 | 673 | 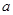 | 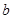 |
| 疫苗无效 | 77 | 90 | 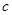 |
(1)现用分层抽样的方法在全体样本中抽取360个测试结果,应在C组抽取样本多少个?
(2)已知
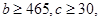 求通过测试的概率.
求通过测试的概率. 天水市第一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,
规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,
得到如下的 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为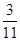 .
.
| | 优秀 | 非优秀 | 合计 |
| 甲班 | 10 | | |
| 乙班 | | 30 | |
| 合计 | | | 110 |
(2)根据列联表的数据,若按99.9%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号。试求抽到9号或10号的概率。
参考公式与临界值表:
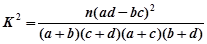 。
。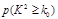 | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
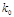 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
第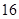 届亚运会于
届亚运会于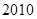 年
年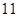 月
月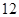 日至
日至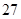 日在中国广州进行,为了做好接待工作,组委会招募了
日在中国广州进行,为了做好接待工作,组委会招募了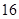 名男志愿者和
名男志愿者和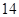 名女志愿者,调查发现,男、女志愿者中分别有
名女志愿者,调查发现,男、女志愿者中分别有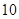 人和
人和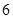 人喜爱运动,其余不喜爱.
人喜爱运动,其余不喜爱.
根据以上数据完成以下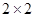 列联表:
列联表:
| | 喜爱运动 | 不喜爱运动 | 总计 |
| 男 | 10 | | 16 |
| 女 | 6 | | 14 |
| 总计 | | | 30 |
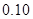 的前提下认为性别与喜爱运动有关?
的前提下认为性别与喜爱运动有关?(3)如果从喜欢运动的女志愿者中(其中恰有
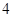 人会外语),抽取
人会外语),抽取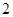 名负责翻译工作,则抽出的志愿者中
名负责翻译工作,则抽出的志愿者中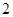 人都能胜任翻译工作的概率是多少?
人都能胜任翻译工作的概率是多少?附:K2=
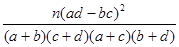
| P(K2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
某种产品的广告费支出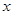 与销售额
与销售额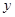 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据:
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |

(1)画出散点图;
(2)求回归直线方程;
(3)试预测广告支出为10百万元时,销售额多大?
(文科)某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本,得频率分布表如下:
| 组号 | 分组 | 频数 | 频率 |
| 第一组 | [230,235) | 8 | 0.16 |
| 第二组 | [235,240) | ① | 0.24 |
| 第三组 | [240,245) | 15 | ② |
| 第四组 | [245,250) | 10 | 0.20 |
| 第五组 | [250,255] | 5 | 0.10 |
| 合 计 | 50 | 1.00 | |
(2)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,分别求第三、四、五各组参加考核人数;
(3)在(2)的前提下,高校决定在这6名学生中录取2名学生,求2人中至少有1名是第四组的概率.

 与身高
与身高 进行测量,得到数据(单位均为
进行测量,得到数据(单位均为 )作为样本如下表所示.
)作为样本如下表所示.
 ;
; ,试估计此人的身高;
,试估计此人的身高; ,
, ,
, ,
, )
)