题目内容
已知命题 命题
命题 ,当命题
,当命题 是真命题,则实数a的取值范围是 ( )
是真命题,则实数a的取值范围是 ( )
A. | B. | C. | D. |
B
解析试题分析:因为命题 ,恒成立,则只要a小于等于
,恒成立,则只要a小于等于 的最小值即可,结合二次函数性质可知,当x=1时取得最小值为2,故a
的最小值即可,结合二次函数性质可知,当x=1时取得最小值为2,故a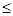 2,
2,
命题 ,说明方程有根,则判别式大于等于零,即为
,说明方程有根,则判别式大于等于零,即为 ,解得为
,解得为 ,
,
当命题 是真命题,说明q,p同时为真,则求解其交集得到为
是真命题,说明q,p同时为真,则求解其交集得到为 ,选B
,选B
考点:本试题主要考查了命题的真假判断与应用。
点评:解决该试题的关键是出两个命题的等价条件以及对且命题的正确理解.同时命题P涉及不等式的恒成立问题的转化求解函数的最小值,命题Q考查了二次方程有无根,通过判别式得到。

练习册系列答案
相关题目
命题:“若x2<1,则-1 ≤ x<1”的逆否命题是
| A.若x2≥1,则x<-1,或x≥1 | B.若-1≤x<1,则x2<1 |
| C.若x≤-1,或x>1,则x2≥1 | D.若x<-1,或x≥1,则x2≥1 |
设条件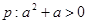 , 条件
, 条件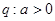 ; 那么
; 那么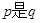 的( )
的( )
| A.充分但不必要条件 | B.必要但不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
特称命题“存在一个被7整除的整数不是奇数”的否定是( )
| A.所有被7整除的整数都不是奇数 |
| B.所有奇数都不能被7整除 |
| C.所有被7整除的整数都是奇数 |
| D.存在一个奇数,不能被7整除 |
若命题“ ”为假,且
”为假,且 为假,则( )
为假,则( )
A.“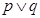 ”为假 ”为假 | B. 假 假 | C. 真 真 | D. 假 假 |
命题“?x>0,x2+x>0”的否定是( ).
A.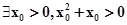 | B.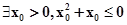 |
| C.?x>0,x2+x≤0 | D.?x≤0,x2+x>0 |
若 ,则“
,则“ ”是“
”是“ ”的( )
”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分又不必要条件 |
下列说法中,正确的是
A.命题“若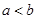 ,则 ,则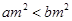 ”的否命题是假命题. ”的否命题是假命题. |
B.设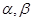 为两个不同的平面,直线 为两个不同的平面,直线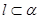 ,则 ,则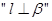 是 是 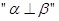 成立的充分不必要条件. 成立的充分不必要条件. |
C.命题“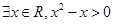 ”的否定是“ ”的否定是“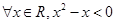 ”. ”. |
D.已知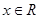 ,则“ ,则“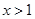 ”是“ ”是“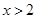 ”的充分不必要条件. ”的充分不必要条件. |
已知 表示两个不同的平面,
表示两个不同的平面, 为平面
为平面 内的一条直线,则“
内的一条直线,则“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |