题目内容
在直四棱柱ABCD-A1B1C1D1中,已知AB∥CD,AB=AD=1,D1D=CD=2,AB⊥AD.(I)求证:BC⊥面D1DB;
(II)求D1B与平面D1DCC1所成角的大小;
(III)在BB1上是否存在一点F,使F到平面D1BC的距离为
 ,若存在,则指出该点的位置;若不存在,请说明理由.
,若存在,则指出该点的位置;若不存在,请说明理由.
【答案】分析:(I)要证BC⊥面D1DB,只需证明直线BC垂直面D1DB内的两条相交直线D1D、DB即可;
(II)取DC中点E,连接BE,D1E.说明∠BD1E为所求角,然后求D1B与平面D1DCC1所成角的大小;
(III)在BB1上是存在一点F,使F到平面D1BC的距离为 ,设BF=x,利用
,设BF=x,利用 求出x的值,即可.
求出x的值,即可.
解答: 解:( I)证明:∵ABCD-A1B1C1D1为直四棱柱,
解:( I)证明:∵ABCD-A1B1C1D1为直四棱柱,
∴D1D⊥平面ABCD,
∴BC⊥D1D.
∵AB∥CD,AB⊥AD.
∴四边形ABCD为直角梯形,
又∵AB=AD=1,CD=2,
可知BC⊥DB.
∵D1D∩DB=D,
∴BC⊥平面D1DB.(4分)
(II)取DC中点E,连接BE,D1E.
∵DB=BC,
∴BE⊥CD.
∵ABCD-A1B1C1D1为直四棱柱,
∴ABCD⊥D1DCC1.
∴BE⊥D1DCC1.
∴D1E为D1B在平面D1DCC1上的射影,
∴∠BD1E为所求角.
在Rt△D1BE中, .
. .
.
∴所求角为 .(9分)
.(9分)
(Ⅲ)假设B1B存在点F,设BF=x,
∵ ,BC⊥平面D1BF,
,BC⊥平面D1BF,
∴ .
.
∵ ,
,
∴ .
.
又 ,
,
∴ .
.
即存在点F为B1B的中点.(14分)
点评:本题考查直线与平面垂直的判定,直线与平面所成的角等知识,考查学生发现问题解决问题的能力,逻辑思维能力,是中档题.
(II)取DC中点E,连接BE,D1E.说明∠BD1E为所求角,然后求D1B与平面D1DCC1所成角的大小;
(III)在BB1上是存在一点F,使F到平面D1BC的距离为
 ,设BF=x,利用
,设BF=x,利用 求出x的值,即可.
求出x的值,即可.解答:
 解:( I)证明:∵ABCD-A1B1C1D1为直四棱柱,
解:( I)证明:∵ABCD-A1B1C1D1为直四棱柱,∴D1D⊥平面ABCD,
∴BC⊥D1D.
∵AB∥CD,AB⊥AD.
∴四边形ABCD为直角梯形,
又∵AB=AD=1,CD=2,
可知BC⊥DB.
∵D1D∩DB=D,
∴BC⊥平面D1DB.(4分)
(II)取DC中点E,连接BE,D1E.
∵DB=BC,
∴BE⊥CD.
∵ABCD-A1B1C1D1为直四棱柱,
∴ABCD⊥D1DCC1.
∴BE⊥D1DCC1.
∴D1E为D1B在平面D1DCC1上的射影,
∴∠BD1E为所求角.
在Rt△D1BE中,
 .
. .
.∴所求角为
 .(9分)
.(9分)(Ⅲ)假设B1B存在点F,设BF=x,
∵
 ,BC⊥平面D1BF,
,BC⊥平面D1BF,∴
 .
.∵
 ,
,∴
 .
.又
 ,
,∴
 .
.即存在点F为B1B的中点.(14分)
点评:本题考查直线与平面垂直的判定,直线与平面所成的角等知识,考查学生发现问题解决问题的能力,逻辑思维能力,是中档题.

练习册系列答案
相关题目
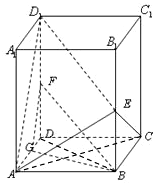 在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、G、F分别是棱B1B、D1D、DA的中点.
在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、G、F分别是棱B1B、D1D、DA的中点.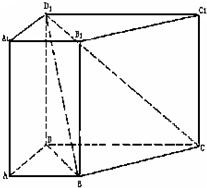 在直四棱柱ABCD-A1B1C1D1中,已知AB∥CD,AB=AD=1,D1D=CD=2,AB⊥AD.
在直四棱柱ABCD-A1B1C1D1中,已知AB∥CD,AB=AD=1,D1D=CD=2,AB⊥AD.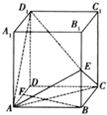 在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、F分别是棱B1B、DA的中点.
在直四棱柱ABCD-A1B1C1D1中,AA1=2,底面是边长为1的正方形,E、F分别是棱B1B、DA的中点. 如图,在直四棱柱ABCD-A1B1C1D1中,点E,F分别在AA1,CC1上,且AE=
如图,在直四棱柱ABCD-A1B1C1D1中,点E,F分别在AA1,CC1上,且AE= 在直四棱柱ABCD-A1B1C1D1中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,AB=AD=1,CD=CC1=2,E为棱AA1的中点,F为棱BB1上的动点.
在直四棱柱ABCD-A1B1C1D1中,底面ABCD为直角梯形,∠BAD=∠ADC=90°,AB=AD=1,CD=CC1=2,E为棱AA1的中点,F为棱BB1上的动点.