题目内容
若直线 与圆
与圆 的两个交点关于直线
的两个交点关于直线 对称,则
对称,则 的值分别为
的值分别为
A. B.
B.
C. D.
D.
【答案】
A
【解析】
试题分析:因为直线y=kx与圆(x-2)2+y2=1的两个交点关于直线2x+y+b=0对称,直线2x+y+b=0的斜率为-2,所以k= ,并且直线经过圆的圆心,所以圆心(2,0)在直线2x+y+b=0上,所以4+0+b=0,b=-4.故选A.
,并且直线经过圆的圆心,所以圆心(2,0)在直线2x+y+b=0上,所以4+0+b=0,b=-4.故选A.
考点:直线与圆的位置关系;关于点、直线对称的圆的方程.
点评:本题考查直线与圆的位置关系,对称直线方程的应用,考查分析问题解决问题与计算能力.

练习册系列答案
相关题目
 的首项为
的首项为 ,公差为
,公差为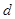 ,其前
,其前 项和为
项和为 ,若直线
,若直线 与圆
与圆 的两个交点关于直线
的两个交点关于直线 对称,则
对称,则 与圆
与圆 有两个不同的交点, 则点
有两个不同的交点, 则点 与圆
与圆 的位置关系是
的位置关系是
 与圆
与圆 有两个不同的交点,则点
有两个不同的交点,则点 圆C的位置关系是
圆C的位置关系是