题目内容
对一切的x∈（0，+∞），3x2+2ax-2xlnx+1≥0恒成立，求实数a的取值范围．
解：∵x＞0，∴3x2+2ax-2xlnx+1≥0可化为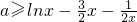
恒成立．（3分）
令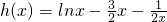
，则
（6分）
令h′（x）＞0，∵x＞0，∴0＜x＜1；
令h′（x）＜0，∵x＞0，∴x＞1，
∴函数在（0，1）上单调递增，在（1，+∞）上单调递减
∴x=1时，h（x）取得最大值-2，（ 10分）
∴a≥-2．
∴a的取值范围是[-2，+∞）． （12分）
分析：先分离参数，再用导数法，求出相应函数的最值，即可求实数a的取值范围．
点评：本题考查导数知识的运用，考查恒成立问题，考查函数的最值，属于中档题．
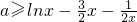恒成立．（3分）令
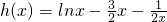，则 （6分）令h′（x）＞0，∵x＞0，∴0＜x＜1；
令h′（x）＜0，∵x＞0，∴x＞1，
∴函数在（0，1）上单调递增，在（1，+∞）上单调递减
∴x=1时，h（x）取得最大值-2，（ 10分）
∴a≥-2．
∴a的取值范围是[-2，+∞）． （12分）
分析：先分离参数，再用导数法，求出相应函数的最值，即可求实数a的取值范围．
点评：本题考查导数知识的运用，考查恒成立问题，考查函数的最值，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目