题目内容
已知函数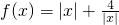 ;当x∈[-3,-1]时,记f(x)的最大值为m,最小值为n,则m+n=________.
;当x∈[-3,-1]时,记f(x)的最大值为m,最小值为n,则m+n=________.
9
分析:由x∈[-3,-1],知|x|∈[1,3],所以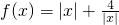 ≥
≥ =4,极大值在区间两端,f(-1)=5,f(-3)=3+
=4,极大值在区间两端,f(-1)=5,f(-3)=3+ ,
,
故f(x)max=5.由此能求出m+n=5+4=9.
解答:∵x∈[-3,-1],
∴|x|∈[1,3],
∴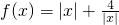
≥ =4,
=4,
当且仅当|x|= ,即|x|=2时,有最小值4.
,即|x|=2时,有最小值4.
极大值在区间两端,f(-1)=5,f(-3)=3+ ,
,
故f(x)max=5.
∴m+n=5+4=9.
故答案为:9.
点评:本题考查函数的最值及詹求法,解题时要认真审题,注意均值不等式的合理运用.
分析:由x∈[-3,-1],知|x|∈[1,3],所以
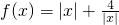 ≥
≥ =4,极大值在区间两端,f(-1)=5,f(-3)=3+
=4,极大值在区间两端,f(-1)=5,f(-3)=3+ ,
,故f(x)max=5.由此能求出m+n=5+4=9.
解答:∵x∈[-3,-1],
∴|x|∈[1,3],
∴
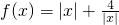
≥
 =4,
=4,当且仅当|x|=
 ,即|x|=2时,有最小值4.
,即|x|=2时,有最小值4.极大值在区间两端,f(-1)=5,f(-3)=3+
 ,
,故f(x)max=5.
∴m+n=5+4=9.
故答案为:9.
点评:本题考查函数的最值及詹求法,解题时要认真审题,注意均值不等式的合理运用.

练习册系列答案
相关题目
已知函数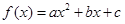 ,当x=1时有最大值1。当
,当x=1时有最大值1。当 时,函数
时,函数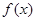 的值域为
的值域为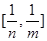 ,则
,则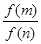 的值为
的值为
A.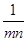 | B.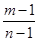 | C.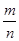 | D.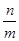 |
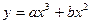 ,当x=
,当x= 1时,有极大值3。(1)求a,b的值;(2)求函数y的极小值。
1时,有极大值3。(1)求a,b的值;(2)求函数y的极小值。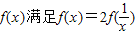 ,当x∈[1,3]时,f(x)=lnx,若在区间
,当x∈[1,3]时,f(x)=lnx,若在区间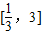 内,函数g(x)=f(x)-ax,有三个不同的零点,则实数a的取值范围是( )
内,函数g(x)=f(x)-ax,有三个不同的零点,则实数a的取值范围是( )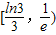
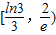
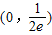
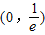
 ,当x∈[1,3]时,f(x)=lnx,若在区间
,当x∈[1,3]时,f(x)=lnx,若在区间 内,函数g(x)=f(x)-ax,有三个不同的零点,则实数a的取值范围是( )
内,函数g(x)=f(x)-ax,有三个不同的零点,则实数a的取值范围是( )



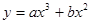 ,当x=1时,有极大值3。(1)求a,b的值;(2)求函数y的极小值。
,当x=1时,有极大值3。(1)求a,b的值;(2)求函数y的极小值。