题目内容
【题目】在底面是菱形的四棱锥P﹣ABCD中,PA⊥底面ABCD,∠BAD=120°,点E为棱PB的中点,点F在棱AD上,平面CEF与PA交于点K,且PA=AB=3,AF=2,则点K到平面PBD的距离为 .
【答案】![]()
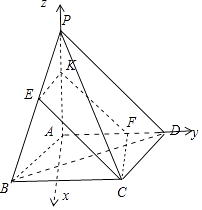
【解析】解:如图所示, 以AP为z轴,AD为y轴,取BC的中点M,以AM为x轴,建立空间直角坐标系.则A(0,0,0),P(0,0,3),D(0,3,0),F(0,2,0),B( ![]() ,﹣
,﹣ ![]() ,0),C(
,0),C( ![]() ,
, ![]() ,0),E(
,0),E( ![]() ,﹣
,﹣ ![]() ,
, ![]() ),
),
设K(0,0,m),则 ![]() =
= ![]() +b
+b ![]() ,
,
∴(0,0,m)= ![]() ,
,
∴ ![]() a﹣
a﹣ ![]() b=0,
b=0, ![]() =0,
=0, ![]() a=m,
a=m,
解得m= ![]() ,a=
,a= ![]() ,b=
,b= ![]() .
.![]() =
= ![]() ,
, ![]() =(0,3,﹣3).
=(0,3,﹣3).
设平面PBD的法向量为 ![]() =(x,y,z),则
=(x,y,z),则 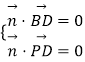 ,
, 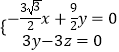 ,
,
取 ![]() =(
=( ![]() ,1,1).
,1,1).![]() =
= ![]() .
.
∴点K到平面PBD的距离d= ![]() =
= ![]() =
= ![]() .
.
所以答案是: ![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目