题目内容
下列函数中，不具有奇偶性的函数是 ( )
A． | B． |
C． | D． |
D
解析试题分析：对A选项，定义域为R，
=
=-(
)=-
，是奇函数；对B选项，要使式子有意义，则
，根据实数商与积的符号法则可化为
，解得
，定义域为（-1,1），=
，∵
=
，根据对数的运算法知==
=-，故是奇函数；对选项C，定义域为R，=
=
=，故是偶函数；对选项D，，=
=
≠，≠-，故不具有奇偶性，故选D.
考点：函数的奇偶性的概念
练习册系列答案
天天向上一本好卷系列答案
相关题目
］=1）,对于给定的n
N*,定义
x
,则当x
时，函数
的值域是（ ）
函数f(x)＝x3＋sin x＋1(x∈R)若f(a)＝2，则f(－a)的值为 ( )．
| A．3 | B．0 | C．－1 | D．－2 |
下列函数中,与函数y=
有相同定义域的是( )
| A．f(x)=lnx | B．f(x)= |
| C．f(x)=|x| | D．f(x)=ex |
成中心对称，且对任意的实数x都有f(x)＝－f
，f(－1)＝1，f(0)＝－2，则f(1)＋f(2)＋…＋f(2013)＝( )
对实数a和b,定义运算“?”:a?b=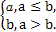
设函数f(x)=(x2-1)?(x-x2),x∈R.若函数y=f(x)-c恰有两个不同的零点,则实数c的取值范围是( )
A．(-∞,-1)∪(- ,0) | B．{-1,-} |
| C．(-1,-) | D．(-∞,-1)∪[-,0) |
函数f(x)=|x|和g(x)=x(2-x)的递增区间依次是( )
| A．(-∞,0],(-∞,1] | B．(-∞,0],[1,+∞) |
| C．[0,+∞),(-∞,1] | D．[0,+∞),[1,+∞) |