题目内容
15.直线l的倾斜角为60°,和直线l平行且经过点(-3,2)的直线方程是( )| A. | y=$\sqrt{3}x+3\sqrt{3}$+2 | B. | y=$\frac{{\sqrt{3}}}{3}x+\sqrt{3}$+2 | C. | y=$\sqrt{3}x-3\sqrt{3}$-2 | D. | y=$\frac{{\sqrt{3}}}{3}x-\sqrt{3}$-2 |
分析 由题意可得斜率等于tan60°,根据点斜式求得直线的方程,再化斜截式方程即可.
解答 解:∵一条直线l的倾斜角为60?,故斜率等于tan60°=$\sqrt{3}$,
和直线l平行且经过点(-3,2)的直线方程是:y-2=$\sqrt{3}$(x+3),即y=$\sqrt{3}x+3\sqrt{3}$+2.
故选:A.
点评 本题主要考查直线的倾斜角和斜率的关系,用点斜式求直线方程,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.已知m、n表示两条不同的直线,α、β表示两个不同的平面,且m⊥α,n?β,则“α⊥β”是“m∥n”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
4.下列说法中一定正确的是( )
| A. | 若a>b,则$\frac{1}{a}$<$\frac{1}{b}$ | B. | 若ac2>bc2,则a>b | C. | 若a>b,则ac>bc | D. | 若a>b,则(${\frac{1}{2}}$)a>(${\frac{1}{2}}$)b |
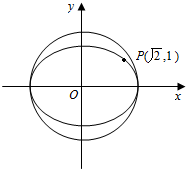 如图,椭圆:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率与双曲线x2-y2=4的离心率互为倒数,且内切于圆x2+y2=4.
如图,椭圆:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率与双曲线x2-y2=4的离心率互为倒数,且内切于圆x2+y2=4.