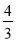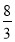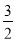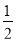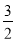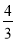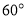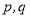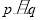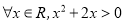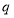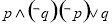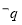题目内容
如图,在四棱锥 中,
中, ⊥平面
⊥平面 ,底面
,底面 为梯形,
为梯形, ∥
∥ ,
, ⊥
⊥ ,
, ,点
,点 在棱
在棱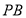 上,且
上,且 .
.

(1)当 时,求证:
时,求证: ∥面
∥面 ;
;
(2)若直线 与平面
与平面 所成角为
所成角为 ,求实数
,求实数 的值.
的值.
(1)证明过程见试题解析;(2)实数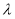 的值为
的值为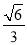 .
.
【解析】
试题分析:(Ⅰ)连接BD交AC于点M,连结ME, 先证明 ,再证明
,再证明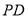 ∥面
∥面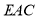 ;
;
先以A为坐标原点,分别以AB,AP为y轴,Z轴建立空间直角坐标系, 求出各点的坐标,再求出平面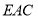 的一个法向量为
的一个法向量为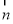 , 而已知直线
, 而已知直线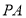 与平面
与平面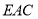 所成角为
所成角为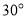 ,进而可求实数
,进而可求实数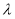 的值.
的值.
试题解析:(Ⅰ)证明:连接BD交AC于点M,连结ME,

因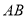 ∥
∥

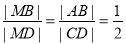 ,当
,当 时
时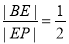 ,
,
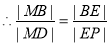

 .
.
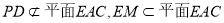
则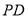 ∥面
∥面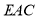 . 4分
. 4分
(Ⅱ)由已知可以A为坐标原点,分别以AB,AP为y轴,Z轴建立空间直角坐标系,设DC=2,则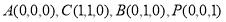 ,
,
由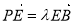 ,可得E点的坐标为
,可得E点的坐标为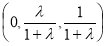 6分
6分
所以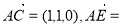
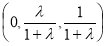 .
.
设平面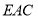 的一个法向量为
的一个法向量为 ,则
,则 ,设
,设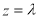 ,则
,则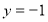 ,
,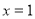 ,所以
,所以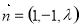 8分
8分
若直线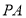 与平面
与平面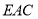 所成角为
所成角为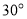 ,
,
则 , 9分
, 9分
解得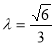 10分
10分
考点:空间向量、直线与平面的位置关系.

练习册系列答案
相关题目