题目内容
甲、乙两人参加某电视台举办的答题闯关游戏,按照规则,甲先从6道备选题中一次性抽取3道题独立作答,然后由乙回答剩余3题,每人答对其中2题就停止答题,即闯关成功.已知在6道被选题中,甲能答对其中的4道题,乙答对每道题的概率都是| 2 | 3 |
(Ⅰ)求甲、乙至少有一人闯关成功的概率;
(Ⅱ)设甲答对题目的个数为X,求X的分布列及数学期望.
分析:(I)由于闯关游戏规则规定甲先从6道备选题中一次性抽取3道题独立作答,然后由乙回答剩余3题,每人答对其中2题就停止答题,即闯关成功,所以可以设甲、乙闯关成功分别为事件A、B,利用对立事件的定义求出甲、乙至少有一人闯关成功的概率;
(II)由于甲答对题目的个数为X,由题意则X的可能取值是1,2,利用随机变量的定义及分布列定义即可求出期望值.
(II)由于甲答对题目的个数为X,由题意则X的可能取值是1,2,利用随机变量的定义及分布列定义即可求出期望值.
解答:解:(Ⅰ)设甲、乙闯关成功分别为事件A、B,
则P(
)=
=
=
,
P(
)=(1-
)3+
(1-
)2=
+
=
,
则甲、乙至少有一人闯关成功的概率是1-P(
•
)=1-P(
)•P(
)=1-
×
=
.
(Ⅱ)因为甲能答对4道题,所以无论怎么选3道题甲至少答对1道题.
所以ξ=1,2,3
P(ξ=1)=(2C2*4C1)/6C3=4/20
P(ξ=2)=(2C1*4C2)/6C3=12/20
P(ξ=3)=(2C0*4C3)/6C3=4/20
由题知X的可能取值是1,2.
P(X=1)=
=
,P(X=2)=
=
,
则X的分布列为
∴EX=1×
+2×
=
.
则P(
. |
| A |
| ||||
|
| 4 |
| 20 |
| 1 |
| 5 |
P(
. |
| B |
| 2 |
| 3 |
| C | 2 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 27 |
| 2 |
| 9 |
| 7 |
| 27 |
则甲、乙至少有一人闯关成功的概率是1-P(
. |
| A |
. |
| B |
. |
| A |
. |
| B |
| 1 |
| 5 |
| 7 |
| 27 |
| 128 |
| 135 |
(Ⅱ)因为甲能答对4道题,所以无论怎么选3道题甲至少答对1道题.
所以ξ=1,2,3
P(ξ=1)=(2C2*4C1)/6C3=4/20
P(ξ=2)=(2C1*4C2)/6C3=12/20
P(ξ=3)=(2C0*4C3)/6C3=4/20
由题知X的可能取值是1,2.
P(X=1)=
| ||||
|
| 1 |
| 5 |
| ||||||
|
| 4 |
| 5 |
则X的分布列为
| X | 1 | 2 | ||||
| P |
|
|
| 1 |
| 5 |
| 4 |
| 5 |
| 9 |
| 5 |
点评:此题重在考查学生对于题意的正确理解,还考查了随机变量的定义及随机变量的分布列,另外还考查了期望与古典概率及独立事件的概率公式.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
 道备选题中一次性抽取
道备选题中一次性抽取 道题独立作答,然后由乙回答剩余
道题独立作答,然后由乙回答剩余
 道题,乙答对每道题
道题,乙答对每道题 .
. 道备选题中一次性抽取
道备选题中一次性抽取 道题独立作答,然后由乙回答剩余
道题独立作答,然后由乙回答剩余 题就停止答题,即闯关成功.已知在
题就停止答题,即闯关成功.已知在 道题,乙答对每道题的概率都是
道题,乙答对每道题的概率都是 .
. 道备选题中一次性抽取
道备选题中一次性抽取 道题独立作答,然后由乙回答剩余
道题独立作答,然后由乙回答剩余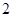
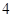 道题,乙答对每道题
道题,乙答对每道题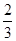 .
. 。(Ⅰ)求甲、乙至少有一人闯关成功的概率;
。(Ⅰ)求甲、乙至少有一人闯关成功的概率; ,求
,求 ,求
,求