题目内容
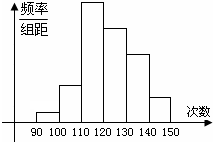为了了解某地高一学生的体能状况，某校抽取部分学生进行一分钟跳绳次数测试，将所得数据整理后，画出频率分布直方图（如图），图中从左到右各小长方形的面积之比为2：4：17：15：9：3，第二小组频数为12．（1）第二小组的频率是多少？样本容量是多少？
（2）若次数在110以上为达标，试估计全体高一学生的达标率为多少？
（3）通过该统计图，可以估计该地学生跳绳次数的众数是
分析：（1）根据从左到右各小长方形的面积之比为2：4：17：15：9：3，第二小组频数为12，用比值做出样本容量．做出的样本容量和第二小组的频率．
（2）根据上面做出的样本容量和前两个小长方形所占的比例，用所有的符合条件的样本个数之和，除以样本容量得到概率．
（3）在频率分布直方图中最高的小长方形的底边的中点就是这组数据的众数，处在把频率分布直方图所有的小长方形的面积分成两部分的一条垂直与横轴的线对应的横标就是中位数．
（2）根据上面做出的样本容量和前两个小长方形所占的比例，用所有的符合条件的样本个数之和，除以样本容量得到概率．
（3）在频率分布直方图中最高的小长方形的底边的中点就是这组数据的众数，处在把频率分布直方图所有的小长方形的面积分成两部分的一条垂直与横轴的线对应的横标就是中位数．
解答：解：（1）∵从左到右各小长方形的面积之比为2：4：17：15：9：3，
第二小组频数为12．
∴样本容量是
=150，
∴第二小组的频率是
=0.08．
（2）∵次数在110以上为达标，
∴在这组数据中达标的个体数一共有17+15+9+3，
∴全体学生的达标率估计是
=0.88 …6分
（3）在频率分布直方图中最高的小长方形的底边的中点就是这组数据的众数，
即
=115，…7分
处在把频率分布直方图所有的小长方形的面积分成两部分的一条垂直与横轴的线对应的横标就是中位数121.3 …8分
第二小组频数为12．
∴样本容量是
| (2+4+17+15+9+3)×12 |
| 4 |
∴第二小组的频率是
| 12 |
| 150 |
（2）∵次数在110以上为达标，
∴在这组数据中达标的个体数一共有17+15+9+3，
∴全体学生的达标率估计是
| 17+15+9+3 |
| 50 |
（3）在频率分布直方图中最高的小长方形的底边的中点就是这组数据的众数，
即
| 110+120 |
| 2 |
处在把频率分布直方图所有的小长方形的面积分成两部分的一条垂直与横轴的线对应的横标就是中位数121.3 …8分
点评：本题考查频率分步直方图的应用，是一个基础题，这种题目解题的关键是看清图中所给的条件，知道小长方形的面积就是这组数据的频率
练习册系列答案
特高级教师点拨系列答案
相关题目
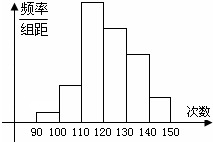为了了解某地高一学生的体能状况，某校抽取部分学生进行一分钟跳绳次数测试，将所得数据整理后，画出频率分布直方图（如图），图中从左到右各小长方形的面积之比为2：4：17：15：9：3，第二小组频数为12．
，第二小组频数为12．
