题目内容
证明：函数f（x）=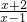
在区间（1，+∞）上的减函数．
证明：函数f（x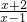）==1+
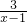的定义域为（-∞，1）∪（1，+∞）．
取x1，x2∈（1，+∞），且x1＜x2，
那么 f（x1）-f（x2）=
∵x2-x1＞0，（x1-1）（x2-1）＞0，
∴f（x1）-f（x2）＞0，
即f（x）在（1，+∞）内是减函数．
分析：先取x1，x2∈（1，+∞），且x1＜x2，然后判定f（x1）-f（x2）的符号，最好根据定义进行判定即可．
点评：本题主要考查了函数的单调性及不等式的基础知识，考查数学推理判断能力，属于基础题．
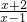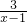=1+的定义域为（-∞，1）∪（1，+∞）．取x1，x2∈（1，+∞），且x1＜x2，
那么 f（x1）-f（x2）=
∵x2-x1＞0，（x1-1）（x2-1）＞0，
∴f（x1）-f（x2）＞0，
即f（x）在（1，+∞）内是减函数．
分析：先取x1，x2∈（1，+∞），且x1＜x2，然后判定f（x1）-f（x2）的符号，最好根据定义进行判定即可．
点评：本题主要考查了函数的单调性及不等式的基础知识，考查数学推理判断能力，属于基础题．
练习册系列答案
长江作业本同步练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
相关题目